La Place des Développeurs Astuce texte 1ère partie
Voici une façon élégante d'afficher des titres sur vos programmes en mode texte.
Pour les explications, voir les commentaires sur le listing basic.

Pour les explications, voir les commentaires sur le listing basic.

Code :
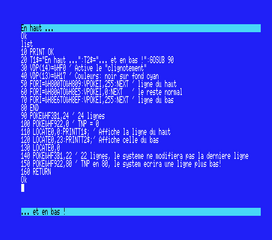
10 SCREEN0:WIDTH80:KEYOFF:COLOR15,4
20 T1$="En haut ...":T2$="... et en bas !":GOSUB 90
30 VDP(14)=&HF0 ' Active le "clignotement"
40 VDP(13)=&H17 ' Couleurs: noir sur fond cyan
50 FORI=&H800TO&H809:VPOKEI,255:NEXT ' ligne du haut
60 FORI=&H80ATO&H8E5:VPOKEI,0:NEXT ' le reste normal
70 FORI=&H8E6TO&H8EF:VPOKEI,255:NEXT ' ligne du bas
80 END
90 POKE&HF3B1,24 ' 24 lignes
100 POKE&HF922,0 ' TNP = 0
110 LOCATE0,0:PRINTT1$; ' Affiche la ligne du haut
120 LOCATE0,23:PRINTT2$;' Affiche celle du bas
130 LOCATE0,0
140 POKE&HF3B1,22 ' 22 lignes, le systeme ne modifiera pas la derniere ligne
150 POKE&HF922,80 ' TNP en 80, le system ecrira une ligne plus bas!
160 RETURN
DONALD TRUMP IS FAST APPROACHING
NEMESIS ! RETURN IMMEDIATELY !
Répondre
Vous n'êtes pas autorisé à écrire dans cette catégorie