Initiation au binaire
Table des matières
Le monde se divise en 10 catégories : ceux qui comprennent le binaire et les autres.
A l'issue de ce module, vous devrez être en mesure de saisir toute la subtilité humoristique de cette phrase culte chez les informaticiens ! Plus sérieusement, le binaire est utilisé en informatique pour une raison simple. Tous les composants d'un ordinateur fonctionnent de la façon suivante : soit le courant passe soit il ne passe pas. Ce qui correspond au 1 / 0 du binaire.
<h1 class="wiki_paragraph1" id="paragraph_rappels-sur-le-systeme-decimal">Rappels sur le système décimal</h1>
<h2 class="wiki_paragraph2" id="paragraph_fonctionnement-du-systeme-decimal">Fonctionnement du système décimal</h2>
Les nombres que nous employons communément sont ceux du système décimal (ou si vous voulez briller en société en base 10
). Cela signifie que tout nombre est décomposable en une somme de puissances de 10.C'est relativement simple : si vous savez faire une multiplication, vous saurez gérer les puissances ! Rien de tel qu'un exemple pour rendre la chose plus concrète : si je prends le nombre 10 000, c'est 10x1000. Ou 10x10x100. Ou encore 10x10x10x10. Ah tiens c'est amusant ça, que des 10 qui se multiplient entre eux !! Eh bien on est en plein dedans, une puissance c'est ça. C'est pour simplifier la notation d'un nombre qui se multiplie par lui-même un certain nombre de fois. Ce nombre de fois est appelé l'exposant. Dans notre exemple, on multiplie 4 fois 10 par lui-même, c'est donc 10 puissance (ou exposant) 4, qu'on notera 104.
D'autres exemples ? 22 c'est 2x2 donc 4. 34 c'est 3x3x3x3 donc 81.
La seule difficulté notable est un nombre mis à la puissance 0. Eh bien figurez vous que n'importe quel nombre mis à la puissance 0 donne 1. 12380 ou 570 donneront toujours 1. C'est comme ça, c'est les mathématiques !
Maintenant qu'on en connaît un peu plus sur les puissances, on va pouvoir attaquer le système décimal de plus près ! Alors pour commencer, dans décimal il y a "déci", comme 10. Ca n'a l'air de rien, mais ça veut tout dire : ça signifie que tout nombre en système décimal (ou base 10) est décomposable en (attention la formule peut paraître compliquée) une somme de produits de puissances de 10.
Bon OK, je vais utiliser un exemple pour être plus parlant : prenons un nombre quelconque, comme 3 752. Eh bien on peut décomposer ce nombre comme suit :
3 752 = 3 000 + 700 + 50 + 2 ou
3 752 = 3x1 000 + 7x100 + 5x10 +2x1 ou encore
3 752 = 3x103 + 7x102 + 5x101 + 2x100
Donc voilà, le système décimal consiste bien en ça. C'est un peu comme si on avait à remplir un tableau avec des cases correspondant aux puissances de 10 :
| 103 | 102 | 101 | 100 |
3 |
7 |
5 |
2 |
Vous remarquerez d'ailleurs que les nombres qui multiplient les puissances de 10 (dans la deuxième ligne du tableau) ne peuvent aller que de 0 à 9, soit au maximum le numéro de la base (ici 10) moins un. On les appelle des digits (rien à voir avec des digitalisations d'image hein
) Ceci est important pour définir le système binaire, que nous aborderons après avoir vu les nombres signés !<h2 class="wiki_paragraph2" id="paragraph_la-problematique-des-nombres-signes">La problématique des nombres signés</h2>
On les appelle aussi "nombres relatifs". Ils sont constitués d'un signe (+ ou -), et d'une partie numérique. Dans la vie de tous les jours, en hiver, vous avez des températures de -5°C par exemple. C'est un nombre signé car, le signe "-" le précède. Les nombres précédés d'un "-" sont dits négatifs, ceux précédés d'un "+" (ou d'aucun signe) sont dits positifs.
Avant d'aborder la partie binaire de la chose, il faut déjà bien maîtriser le principe en système décimal. C'est pourquoi il va falloir connaitre les opérations de base et un peu de vocabulaire sur ces nombres signés :
Tout d'abord, il faut savoir que les nombres signés qui ont la même partie numérique, mais de signe différents sont dits nombres opposés. De plus, la somme de deux nombres opposés est égale à 0. Un peu de "concrétitude" ?
Il fait -5°C dehors. On nous dit à la météo qu'il fera demain 5°C de plus, on arrive bien à une température de 0°C. Donc (-5) + (+5) = 0.
<h3 class="wiki_paragraph3" id="paragraph_addition">Addition</h3>
Ca se complique un peu : le signe va jouer grandement dans le résultat de l'addition ! Si on additionne deux nombres de même signe, aucun problème : on garde le signe des nombres, et on additionne la partie numérique. Exemples :
(-6) + (-3) = -9
(+5) + (+4) = 9 (ou +9)
Pour les additions de nombres de signes opposés, il faut d'abord regarder celui qui a la plus grande partie numérique. Le signe de la somme sera celui de ce nombre. Pour la partie numérique de la somme, on fait la soustraction du nombre à la partie numérique la plus grande par la partie numérique du deuxième. Allez, quelques exemples pour illustrer tout ça !
(-36) + (+12) : le nombre de plus grande partie numérique est -36. Le signe de la somme sera donc négatif. Partie numérique : 36 - 12 = 24. Le résultat de la somme est donc -24.
(-15) + (+27) : le nombre de plus grande partie numérique est +27. Le signe de la somme sera donc positif. Partie numérique : 27 - 15 = 12. Le résultat de la somme est donc 12.
<h3 class="wiki_paragraph3" id="paragraph_soustraction">Soustraction</h3>
Pour les nombres signés je vais vous en dire une bien bonne, il faut transformer la soustraction en addition ! Pour réaliser ce prodige mathématique, il suffit de remplacer le nombre soustrait par son opposé ! Exemple :
(-4) - (-5) = (-4) + (+5) = 1
D'ailleurs, à partir de maintenant, et grâce à cet exemple, on partira du principe que soustraire un nombre c'est ajouter son opposé.
<h3 class="wiki_paragraph3" id="paragraph_multiplication-et-division">Multiplication et division</h3>
Pour ces deux opérations, ce qui se passe entre les parties numériques reste le même que pour les nombres non signés. Toute la subtilité se trouve dans les signes !
Quand on multiplie ou divise deux nombres positifs, pas de problème, c'est un nombre positif. Exemple: (+4) x (+3) = +12
Par contre, quand on divise ou multiplie deux nombres négatifs, on obtient... un nombre positif ! (-4) x (-2) = +8 par exemple.
Enfin, quand on multiplie ou divise un nombre positif et un nombre négatif, le signe du résultat est toujours négatif ! (-3) x (+5) = -15.
<h1 class="wiki_paragraph1" id="paragraph_le-systeme-binaire">Le système binaire</h1>
<h2 class="wiki_paragraph2" id="paragraph_fonctionnement-du-systeme-binaire">Fonctionnement du système binaire</h2>
Alors le binaire... Eh bien à la place de compter en puissances de 10 comme on le fait dans le système décimal, on va compter en puissances de 2 ! Et si vous avez bien suivi, si on reprend le tableau qu'il y avait plus haut dans le système décimal, les cases ne seront remplies que par des 0 ou des 1 ! D'ailleurs - un peu de vocabulaire informatique en passant ne peut pas faire de mal - les digits en binaire sont appelés bits (contraction de l'anglais binary digits). Tout nombre est donc décomposable en puissances de 2. Prenons le nombre 37 par exemple, en binaire il s'écrira 100101. En réutilisant le tableau, on comprend immédiatement pourquoi :
| 25 | 24 | 23 | 22 | 21 | 20 |
1 |
0 |
0 |
1 |
0 |
1 |
On a bien 37 = 1x25 + 0x24 + 0x23 + 1x22 + 0x21 + 1x20
Soit 37 = 32 + 0 + 0 + 4 + 1
De même, 29 sera noté en binaire 11101 :
29 = 16 + 8 + 4 + 1
29 = 1x24 + 1x23 + 1x22 + 0x21 + 1x21
Vous avez saisi le principe ? J'espère, car on va aborder les opérations sur ces nombres binaires, et là ça se complique un tantinet !
D'autant qu'en plus des opérations arithmétiques "classiques" (addition, soustraction...) les nombres en binaire peuvent également être soumis à des opérations dites logiques !<h2 class="wiki_paragraph2" id="paragraph_operations-arithmetiques">Opérations arithmétiques</h2>
<h3 class="wiki_paragraph3" id="paragraph_addition">Addition</h3>
Pour additionner deux nombres en binaire, c'est le même principe que l'addition de nombre décimaux ! Petit rappel de ce principe : vous additionnez les digits des nombres de droite à gauche, avec le principe de retenue quand vous dépassez ou égalez 10. Exemple :
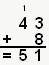
En binaire, vous aurez la retenue dès que vous égalez 2 (je-pose-0-et-je-retiens-1), ce qui arrive uniquement lorsque vous ajoutez deux 1 ! La preuve, en binaire : 1 + 1 = 10 !! (l'occasion de comprendre la citation de début de cours d'ailleurs
)Après, l'addition se comporte de façon classique : 1+0 ou 0+1 font 1 et 0+0=0 (et non pas la tête à Toto comme on a déjà dû essayer de vous le faire croire
).Faites bien attention lorsque vous avez plusieurs retenues (type une addition de 4 nombres) !
Allez, on se refait notre petit exemple (en binaire cette fois) pour bien saisir la méthode. Reprenons 43 et 8, respectivement 101011 et 1000. On positionne notre addition :
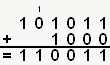
Et si vous convertissez 110011 en décimal, vous trouvez bien 51, c'est
<h3 class="wiki_paragraph3" id="paragraph_soustraction">Soustraction</h3>
Pour la soustraction, c'est pareil, on procède comme en décimal (on soustrait les bits de droite à gauche), mais en faisant bien attention à ne pas oublier la retenue lorsqu'on à un 0-1 ! Un exemple tout bête pour illustrer le propos : 10-1. Soit 2-1 en décimal. Le résultat est bien 1.
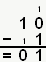
<h3 class="wiki_paragraph3" id="paragraph_multiplication">Multiplication</h3>
Alors pour la multiplication, rien de plus facile : c'est strictement le même que pour la multiplication décimale ! Il ne vous reste plus après qu'à réaliser les additions suivant la techniques décrite précédemment !
Un exemple ? OK ! 5x3 ça vous va ? Donc 101x11 en binaire. Je pose l'opération :
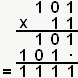
Super simple non ?
<h3 class="wiki_paragraph3" id="paragraph_division">Division</h3>
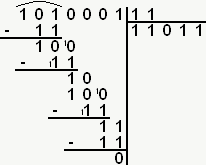
Pour la division binaire, c'est toujours le même principe : on procède comme en décimal lorsqu'on pose l'opération. Maintenant que vous savez comment faire une soustraction, il ne devrait pas y avoir de problème !
Dans l'exemple ci-dessous, je divise 81 par 3, en convertissant le résultat binaire, j'obtiens bien 27.
<h2 class="wiki_paragraph2" id="paragraph_nombres-signes-en-binaire">Nombres signés en binaire</h2>
Nous revenons à présent aux nombres signés... Mais en binaire cette fois ! Comment fait-on pour marquer le signe d'un nombre binaire ?
Eh bien, absolument pas !
Déjà, il ne faut pas oublier que votre MSX ne connaît en réalité que les 0 ou les 1. Donc pas les" +" ou les "-"... Alors comment faire ? Eh bien en utilisant avant le nombre un 1 ou un 0 ! Un nombre positif sera codé avec un 0, un nombre négatif avec un 1.Malheureusement, non. Ou plutôt pas vraiment... Pourtant j'ai bien mis un 1 avant la valeur... Mais si vous additionnez les deux opposés, vous devriez trouver 0, ce qui n'est pas le cas ici (100). La solution réside, en premier lieu, dans le nombre de bits sur lequel on prend le nombre !! On entre là dans des considérations un poil plus complexes, mais pas inabordables !
Imaginons que nous nous restreignons à avoir des nombres (non signés) représentés sur 8 bits maximum (comme un peu de vocabulaire ne fait pas de mal, un octet = 8 bits), si tous les bits sont à 1, le plus grand nombre possible est donc 255 : 27 + 26 + 25 + 24 + 23 + 22 + 21 + 20 = 128 + 64 + 32 + 16 + 8 + 4 + 2 +1.
| bit 7 | bit 6 | bit 5 | bit 4 | bit 3 | bit 2 | bit 1 | bit 0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Alors immédiatement une petite remarque pour commencer, on considère toujours que le premier bit est le bit 0, et il est toujours celui situé le plus à droite. Notez bien cet état de fait, cela pourra vous resservir si vous osez vous frotter aux registres du Z80 ou des VDP de vos MSX !!
Revenons à notre nombre binaire sur un octet donc. Le bit 7 est donc le bit du signe, OK. Les 7 autres bits coderont donc le nombre sur lequel on appliquera l'opération. Bien entendu, le maximum possible sera forcément plus petit, cette fois ce sera 127 (je ne vous refais pas le calcul, mais vous pouvez me faire confiance
).Alors allons-y, je vas enfin pouvoir passer en binaire euh... allez, -7 par exemple !! Je suis donc le raisonnement : sur 8 bits j'ai donc pour 7 : 00000111, et pour -7 je devrais avoir 10000111. Comme la somme de deux nombres opposés est nulle, je vais immédiatement vérifier le résultat :
Oui surprenant n'es-ce pas
? Bon j'avoue ne pas avoir tout dit, il y a encore quelques subtilités pour représenter un nombre négatif en binaire... Deux subtilités pour être précis. Ce qui a été dit précédemment est toujours valable, à savoir que dorénavant, le bit 7 définira bien le signe de notre nombre, ça c'est immuable. Par contre, l'ajout de ce signe se produit lors d'une transformation que l'on appelle le complément à 1. Pas de problème, je vous explique tout ça de suite : le complément à 1 consiste tout simplement à transformer un nombre binaire en changeant les valeurs des bits qui le composent ! Ainsi les 1 deviennent 0 et les 0 deviennent 1 ! Pour réaliser le complément à 1 de 7, on a donc 00000111 qui devient 11111000. Facile non ?
La dernière transformation à effectuer est d'ajouter 1. On appelle ça le complément à 2. Notre transformation précédente donne ainsi 11111001. Et là on tient ENFIN notre opposé !!
Il y a une dernière petite remarque à faire, pour ceux qui auraient l'idée d'ajouter deux opposés pour vérifier le résultat : vous aurez toujours un petit 1 dont vous ne saurez quoi faire à la fin de votre opération, une retenue qui ne sera pas quantifiée selon le nombre de bits sur lequel vos nombres sont représentés. Pour le moment : N'EN TENEZ PAS COMPTE !
Bien évidemment, cette manière de représenter les nombres binaires signés aura une incidence sur les opérations arithmétiques de base, mais je vais m'empresser de vous donner les tuyaux pour ne pas rater vos calculs !
<h3 class="wiki_paragraph3" id="paragraph_addition-et-soustraction">Addition et soustraction</h3>
Ô joie, ô bonheur ! Pour l'addition, rien ne change ! Qu'on additionne un nombre négatif à un positif, ou deux négatifs entre eux (je ne parle pas de la somme de deux positifs, déjà abordée), le résultat est bon sans qu'il y ait à revoir quoi que ce soit !
Additionnons par exemple -2 et 3, puis -2 et -3. Allez, révision immédiate pour obtenir -2 et -3 ! Sur un octet, 2 se code 00000010. Son complément à 1 est donc 11111101, et donc son complément à 2 11111110. De même, 3 est codé 00000011, son complément à 1 est donc 11111100, et son complément à 2 11111101. On pose nos additions ? Allons-y !
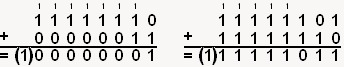
Les parenthèses sont là pour indiquer le dernier bit de retenue, qui en dehors de notre représentation sur 8 bits. Vous vous apercevez donc bien que les additions donnent les bons résultats.
La soustraction à présent... Est-ce que vous vous souvenez de ce que j'avais dit plus haut ? Qu'en fait une soustraction n'est rien d'autre qu'une "addition déguisée" ? Que si je fais 2-3 c'est comme si je faisais 2 + (-3) ? Eh bien c'est la règle qu'on applique pour la soustraction en binaire signé ! C'est clairement beaucoup plus simple d'emploi !
<h3 class="wiki_paragraph3" id="paragraph_multiplication-et-division">Multiplication et division</h3>
Pour la multiplication, idem, l'opération se passe comme pour les binaires non signés. Ceci dit, vu ce qu'on connaît de la multiplication de nombres signés dans le système décimal, on peut utiliser une astuce pour faciliter et réduire les calculs lors de la multiplication de deux nombres négatifs : on sait que la multiplication de deux nombres négatifs donnera un nombre positif, par exemple (-2)x(-3) donnera 6. Or, le produit de leurs opposés donne également le même résultat : 2x3 = 6. Donc, lorsque vous avez deux binaires négatifs à multiplier, prenez leur compléments à 2 avant de réaliser l'opération, vous gagnerez du temps !
Enfin, la division est l'opération qui est la plus problématique avec les binaires signés. En effet, si vous vous amusez à poser une division entre nombres négatifs, ou entre un nombre positif et un négatif, ou encore un négatif et un positif, vous ne parviendrez à aucun résultat valable !
La méthode à employer est la suivante :
Les deux nombres sont négatifs
De même que pour la multiplication, diviser deux nombres négatifs donne un positif. Par conséquent, il suffit de prendre les compléments à 2 des deux nombres de l'opération pour réaliser la division et vous aurez votre résultat !
L'un des deux nombres est négatif
Nous avons là le cas le plus complexe, je réclame donc toute votre attention !
La première chose à faire est de remplacer le nombre négatif de l'opération par son complément à 2.
Ensuite, vous réalisez votre division, qui deviendra une division de deux nombres positifs, donc un cas qu'on a déjà abordé auparavant.
Enfin, le vrai résultat de l'opération sera le complément à 2 du résultat de la division précédente.
Je sens que vous mourez d'envie d'avoir un exemple : on y va donc. Nous allons diviser 14 par -2 (si vous avez tout bien suivi, on doit obtenir comme résultat final -7). En binaire j'ai : 00001110 divisé par 11111110. On y va donc :
1ère étape :
complément à 2 du nombre négatif, ici 11111110, j'obtiens donc 00000010
2ème étape :
Je divise 1110 par 10. On pose l'opération :
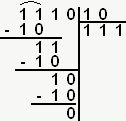
3ème étape :
Je prends le complément à 2 de mon résultat précédent (111). Je trouve 11111001, ce qui est bien l'écriture en binaire de -7 sur un octet. Mission accomplie !
Les deux nombres sont positifs
C'est le cas que nous avions déjà abordé auparavant avant de voir les nombres signés en binaire, je ne m'étends donc pas plus sur le sujet.
Voilà pour ce qui concerne les nombres signés, et les opérations arithmétiques qui s'appliquent sur ces nombres. Nous allons maintenant aborder une partie différente, les opérations logiques !!
<h2 class="wiki_paragraph2" id="paragraph_operations-logiques">Opérations logiques</h2>
Avant d'aborder les opérations logiques en elles-même, il faut peut-être expliquer leur utilité, en tout cas pour ce qui va nous intéresser par la suite : la programmation. Il pourra vous arriver dans un programme d'avoir à réaliser des tests ou même des combinaisons de tests (et ce assez souvent, faites-moi confiance !).
Ainsi, telle ou telle partie d'un programme ne s'exécutera que si une ou plusieurs conditions particulières sont réalisées. Ces tests auront des résultats assez, disons... limités, vu qu'ils seront soit vrais, soit faux. Aucune autre possibilité...
Comme le monde est (parfois) bien fait, 2 valeurs possibles, c'est exactement pareil que les bits possibles en binaire : 0 ou 1. Pas la peine d'insister, vous comprendrez facilement alors que le binaire sera donc aussi utilisé pour « coder » les résultats de tests. Le 0 codera le résultat « faux », le 1 le résultat « vrai ».
Essayons de rendre ça un peu plus compréhensible avec un exemple concret : prenons la phrase « J'ai les yeux verts ». Suivant les personnes, cette phrase (qu'on appellera assertion) est vraie ou fausse. Si j'ai effectivement les yeux verts, l'assertion est vraie, elle sera codée sous forme d'un 1. Si j'ai les yeux bleus, ou marron, l'assertion est alors fausse, et codée par un 0.
On résume :
une assertion vérifiée prend comme valeur binaire 1
une assertion fausse prend comme valeur binaire 0
A quoi vont nous servir les opérateurs logiques donc ? Eh bien à renvoyer une et une seule valeur pour les différentes assertions ou combinaisons d'assertions rencontrées au cours d'un programme ! Vous êtes prêts à attaquer ?
<h3 class="wiki_paragraph3" id="paragraph_l-operateur-not">L'opérateur NOT</h3>
Nous allons donc aborder le premier opérateur logique ! Ce n'est pas le plus dur, vu qu'il ne s'applique qu'à un seul nombre ! Si vous parlez le strict minimum en anglais, vous aurez compris le sens de celui-ci : la négation !
Reprenons mon exemple de toute à l'heure : « J'ai les yeux verts » : la négation de cette assertion est bien « Je n'ai pas les yeux verts ». Analysons un peu ce qui se passe sur nos valeurs binaires :
J'ai effectivement les yeux verts : « J'ai les yeux verts » renvoie 1, mais « Je n'ai pas les yeux verts » renvoie 0
J'ai les yeux bleus : « J'ai les yeux verts » renvoie 0, mais « Je n'ai pas les yeux verts » renvoie 1
Si on observe attentivement, on se rend facilement compte que la négation appliquée à une valeur binaire a comme effet de la transformer en son complément à 1 (vous vous souvenez ? Le 1 devient 0 et le 0 devient 1) !
On va résumer ça dans un joli tableau, qu'on appelle table de vérité. Ces tableaux sont très utiles pour résumer les actions des opérateurs logiques. On va prendre la lettre A pour définir la valeur de notre assertion.
Table de vérité du NOT |
|
|---|---|
A |
NOT A |
0 |
1 |
1 |
0 |
Voilà, on a vu notre premier opérateur logique, le plus facile à saisir. Maintenant, on va pouvoir aborder les opérateurs entre 2 valeurs binaires.
<h3 class="wiki_paragraph3" id="paragraph_l-operateur-and">L'opérateur AND</h3>
On continue notre révision du cours d'anglais de 6ème : AND est donc l'opérateur logique qui représente le ET. On prend encore un exemple pour illustrer le propos ? OK !
Alors disons que je cherche la femme parfaite
. Pour moi, cette femme parfaite est blonde aux yeux bleus, je ne choisirai pas de femme avec d'autres critères physiques. J'ai donc 2 assertions à vérifier : « une femme blonde » et « une femme aux yeux bleus ». J'ai donc 4 possibilités :la femme est blonde aux yeux bleus
la femme est blonde et n'a pas les yeux bleus
la femme n'est pas blonde aux yeux bleus
la femme n'est pas blonde et n'a pas les yeux bleus
On voit que seule la première proposition est celle que je recherche ! Donc le résultat de l'opérateur ET n'est vrai que si les 2 assertions sont vraies également. Dans tous les autres cas, le résultat sera faux. Allons-y pour le tableau de vérité de l'opérateur (cette fois, on prend A pour la première assertion, B pour la deuxième) :
Table de vérité du AND |
||
|---|---|---|
A |
B |
A AND B |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Si ça va, on continue avec l'opérateur suivant !
<h3 class="wiki_paragraph3" id="paragraph_l-operateur-or">L'opérateur OR</h3>
On va commencer à avoir un peu plus de subtilité au niveau des opérateurs... Le OR représente le OU (je vous laisse traduire comme des grands maintenant
), mais le OU dit inclusif.Expliquons cette petite subtilité. Lorsque vous êtes confronté à un choix entre deux éléments, généralement, vous en prenez un, et un seul. Le OU inclusif quant à lui permet de prendre les deux !
Encore un petit exemple pour illustrer tout ça. Je suis à la fin d'un repas, et on me propose fromage ou dessert... L'important étant que je prenne quelque chose. J'ai donc l'assertion « Je prends du fromage » et l'assertion « Je prends du dessert ». Suivant mon choix, j'aurai donc 4 possibilités pour le résultat de mon opération logique :
Je ne prends pas de fromage, ni de dessert
Je ne prends pas de fromage, uniquement du dessert
Je prends du fromage, mais pas de dessert
Je prends du fromage et du dessert
Ici, je vois que le fait d'avoir pris quelque chose n'est vérifié que dans les propositions 2, 3 et 4 ! On y va pour le tableau de vérité ?
Table de vérité du OR |
||
|---|---|---|
A |
B |
A OR B |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
<h3 class="wiki_paragraph3" id="paragraph_l-operateur-xor">L'opérateur XOR</h3>
Rien à voir avec le célèbre shérif de l'espace... Cet opérateur représente cette fois le OU exclusif, où contrairement à son prédécesseur, pour u choix entre deux éléments, on ne peut en prendre qu'un et un seul. Je reprends mon exemple pour le OR, en imaginant cette fois que mes choix soient dictés par un menu au restaurant. Je ne peux vraiment avoir QUE fromage ou QUE dessert, ou rien. Le fait que je prenne quelque chose, en ayant le droit de le faire, est résumé par les mêmes propositions que précédemment :
Je ne prends pas de fromage, ni de dessert
Je ne prends pas de fromage, uniquement du dessert
Je prends du fromage, mais pas de dessert
Je prends du fromage et du dessert
Les seuls cas où je prends quelque chose en ayant le droit de le faire sont les propositions 2 et 3. Dans la première proposition, je ne prends rien, et dans la quatrième, j'en prends trop ! Voici donc la table de vérité de l'opérateur XOR
Table de vérité du XOR |
||
|---|---|---|
A |
B |
A XOR B |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
<h3 class="wiki_paragraph3" id="paragraph_l-operateur-imp">L'opérateur IMP</h3>
On va aborder des notions nettement plus complexes ou abstraites avec cet opérateur...
IMP est l'opérateur d'implication. Ici on va entrer dans des conditions plus ou moins... mathématiques. On va prendre 2 assertions, qu'on appellera A et B. A implique B signifie que B est une condition nécessaire pour A, est que A est une condition suffisante pour B.
Pour expliciter tout ça je prends un exemple plus concret. Entre amis, on s'est fixé une règle : le dernier arrivé paie l'apéro...
.Ici mes assertions sont « Je suis le dernier arrivé » et « je paie l'apéro ». Voyons donc les possibilités :
Je ne suis pas le dernier, je ne paie pas l'apéro. Le résultat de l'implication est bien vérifié ! En effet, si on décide d'attendre le dernier pour payer son verre, la règle est bien respectée !
Je ne suis pas le dernier, mais je paie quand même l'apéro. Ici, le résultat de l'implication est VRAI aussi, car rien ne m'empêche de payer l'apéro en dehors du fait que j'arrive le dernier (juste parce que je suis bien sympa
).Je suis le dernier arrivé, et je paie l'apéro : aucun problème, la règle est respectée aussi.
Je suis le dernier arrivé, je refuse de payer l'apéro : là il y a problème car la règle n'est pas respectée ! L'implication est donc fausse !
Résumons tout ça dans la table de vérité de l'opérateur :
Table de vérité du IMP |
||
|---|---|---|
A |
B |
A IMP B |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
<h3 class="wiki_paragraph3" id="paragraph_l-operateur-eqv">L'opérateur EQV</h3>
Cet opérateur représente cette fois l'équivalence. Si on a deux assertions, le résultat de l'équivalence n'est vrai que si les deux assertions sont dans le même état ! C'est relativement simple à comprendre. Prenons par exemple les assertions suivantes : « Il fait beau » et « Le soleil brille ». Voyons alors les 4 possibilités habituelles :
Il fait beau, le soleil brille. En effet, si le soleil brille, il fait forcément beau : les assertions sont bien équivalentes !
Il fait beau, le soleil ne brille pas. Là, on a une contradiction évidente, l'équivalence n'est pas respectée.
Il ne fait pas beau, le soleil brille. Même cas de situation que précédemment, l'équivalence n'est pas respectée
Il ne fait pas beau, le soleil ne brille pas. S'il ne fait pas beau, pas de soleil, l'équivalence est bien respectée.
Résumons ça dans la table de vérité qui va bien :
Table de vérité du EQV |
||
|---|---|---|
A |
B |
A EQV B |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Voilà, le tour des opérateurs logiques usuels est réalisé, sachant que les deux derniers ne seront que peu utilisés en comparaison des précédents. Il nous reste à aborder un dernier point, à titre informatif, et ce sera terminé de cette initiation au binaire !
<h3 class="wiki_paragraph3" id="paragraph_operateurs-logiques-appliques-aux-nombres">Opérateurs logiques appliqués aux nombres</h3>
Les opérateurs que nous venons de voir ne concernaient ici que des conditions, soit des opérations sur un seul bit. Eh bien figurez vous que vous pouvez appliquer ces mêmes opérateurs... sur des nombres. Quel intérêt ? Eh bien il est peut-être un peu tôt pour vous l'expliquer (ou comment se débarrasser d'une question embarrassante
), mais ils peuvent s'avérer utiles pour modifier certaines valeurs par exemple. On va voir immédiatement comment fonctionnent ces opérateurs sur des nombres.Bien évidemment, ces opérateurs vont concerner les représentations binaires des nombres. Avant de faire un 2 XOR 4, il vous faudra donc convertir les valeurs en binaire. Eh bien, tant qu'on a un exemple, allons y.
Sur un octet, j'ai donc 2 qui est représenté par 00000010 et 4 par 00000100.
La règle est la suivante : lorsqu'on applique un opérateur logique à un nombre binaire, le résultat est application de l'opérateur bit par bit correspondant.
Je dois donc réaliser toutes les opérations suivantes :
- bit 7 du premier nombre XOR bit 7 du deuxième nombre
- bit 6 du premier nombre XOR bit 6 du deuxième nombre
- bit 5 du premier nombre XOR bit 5 du deuxième nombre
- …
- bit 0 du premier nombre XOR bit 0 du deuxième nombre
Si j'applique ma méthode, je trouverai donc 00000110, soit 6 !
Avec l'opérateur AND, j'aurais trouvé 0, et avec l'opérateur OR, 6. L'opérateur IMP m'aurait renvoyé -3, et l'opérateur EQV -7 !
Voilà qui termine ce cours d'initiation au binaire, en espérant que vous y avez trouvé des informations intéressantes !
Vous voilà maintenant prêts à attaquer une autre représentation des nombres : l'hexadécimal !
<h1 class="wiki_paragraph1" id="paragraph_annexe">Annexe</h1>
En annexe, voici quelques puissances de 2 qu'il vous sera utile de connaître (par coeur de préférence
) :- 20 = 1
- 21 = 2
- 22 = 4
- 23 = 8
- 24 = 16
- 25 = 32
- 26 = 64
- 27 = 128
- 28 = 256
- 29 = 512
- 210 = 1024
- 211 = 2048
- 212 = 4096
- 213 = 8192
- 214 = 16 384
- 215 = 32 768