Initiation à l'hexadécimal

Introduction

Derrière ce nom particulièrement barbare se cache une nouvelle manière de représenter les nombres, en dehors de la représentation traditionnelle en décimal, ou de la représentation binaire, certes la plus "proche" de l'ordinateur, mais assez lourde à gérer pour les grands nombres. Pour bien assimiler ce qui sera dit, je vous invite à consulter les paragraphes concernant le fonctionnement de ces deux systèmes dans le cours sur le binaire.

Fonctionnement du système hexadécimal

On a donc le système décimal, à base de puissances de 10, le système binaire à base de puissances de 2, et maintenant le système hexadécimal à base de puissances de... 16 !



16 !!! Quelle idée bizarre ! Pourquoi ce nombre et pas un autre ?



C'est très simple. La mesure en informatique, c'est l'octet (huit bits). Les nombres ainsi codés iront au maximum (si on ne prend pas en compte les nombres signés, donc uniquement des nombres positifs) jusqu'à 11111111, soit 255. Calculez à présent 2⁸. Vous trouvez 256. Tiens ça c'est amusant... ou plutôt totalement logique En effet, si on ajoute 1 à 11111111, on trouve 100000000 ! On aurait un bit 8, correspondant à 2⁸. Et le 8 qui est en exposant... N'est-ce pas par le plus grand hasard le nombre de bits sur lequel on code un octet ? Bingo ! Dans 2⁸, le chiffre 2 représente la base, l'exposant 8, le nombre de digits pour écrire les nombres !





Reprenons notre 2⁸.

On peut l'écrire 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2.

Ou bien encore (2 x 2) x (2 x 2) x (2 x 2) x (2 x 2).

Donc 4 x 4 x 4 x 4.

Ou si vous préférez (4 x 4) x (4 x 4)

Et finalement 16 x 16, ou 16² !



Si je suis le raisonnement pour le binaire js suis en base 16, pour coder un nombre sur un octet, j'utiliserai donc seulement 2 digits !! Voilà tout l'intérêt de travailler en base 16 ! 2 digits au lieu de 8, c'est beaucoup plus facile !



Passons justement aux digits en hexadécimal. Comme vous le savez, un digit est représenté par un chiffre, ayant une valeur maximale de (valeur de la base) - 1. Ici en base 16, on aurait au maximum 15.



Oui mais 15 ce n'est pas un chiffre !! Comment faire alors ?



C'est là qu'intervient toute la subtilité : pour représenter les digits dont les valeurs dépassent 9, on va utiliser... les lettres de l'alphabet ! Quand je compterai en hexadécimal jusqu'à 15 j'aurai donc : 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E et F !

Opérations en hexadécimal

Comme on l'a vu dans l'initiation au binaire, les opérations arithmétiques de base doivent répondre aux spécificités de la base dans laquelle on se trouve. Cependant, les principes mêmes des opérations sont les mêmes qu'en décimal, il reste juste à savoir les valeurs particulières !

En ce qui concerne les nombres signés, l'hexadécimal n'étant qu'une "simplification" du binaire, les particularités vues auparavant s'appliqueront aussi en hexadécimal.



Je vais ainsi vous livrer 3 tableaux qui pourront s'avérer fort utiles par la suite :



Le premier est un tableau de conversion multi-systèmes :

Valeur décimale	Valeur binaire	Valeur hexadécimale
0	0	0
1	1	1
2	10	2
3	11	3
4	100	4
5	101	5
6	110	6
7	111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F

Le tableau suivant est une table d'addition.

+	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10
2	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11
3	4	5	6	7	8	9	A	B	C	D	E	F	10	11	12
4	5	6	7	8	9	A	B	C	D	E	F	10	11	12	13
5	6	7	8	9	A	B	C	D	E	F	10	11	12	13	14
6	7	8	9	A	B	C	D	E	F	10	11	12	13	14	15
7	8	9	A	B	C	D	E	F	10	11	12	13	14	15	16
8	9	A	B	C	D	E	F	10	11	12	13	14	15	16	17
9	A	B	C	D	E	F	10	11	12	13	14	15	16	17	18
A	B	C	D	E	F	10	11	12	13	14	15	16	17	18	19
B	C	D	E	F	10	11	12	13	14	15	16	17	18	19	1A
C	D	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B
D	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C
E	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C	1D
F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C	1D	1E

Enfin, ceci est le tableau de multiplication.

x	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
1	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
2	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E
3	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D
4	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C
5	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B
6	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A
7	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69
8	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78
9	9	12	1B	24	2D	36	3F	48	51	5A	63	6C	75	7E	87
A	A	14	1E	28	32	3C	46	50	5A	64	6E	78	82	8C	96
B	B	16	21	2C	37	42	4D	58	63	6E	79	84	8F	91	A5
C	C	18	24	30	3C	48	54	60	6C	78	84	90	9C	A8	B4
D	D	1A	27	34	41	4E	5B	68	75	82	8F	9C	A9	B6	C3
E	E	1C	2A	38	46	54	62	70	7E	8C	9A	A8	B6	C4	D2
F	F	1E	2D	3C	4B	5A	69	78	87	96	A5	B4	C3	D2	E1

Grâce à ces tableaux, vous pourrez réaliser la plupart des opérations courantes. Allons-y pour leur descriptif !

Addition

Pour réaliser une addition, on prend les mêmes règles que d'habitude, donc comme en décimal ou en binaire. C'est là aussi que le tableau d'addition va nous servir (le fait que F + F = 1E n'est pas forcément facile à retenir ). Donc quand on pose son opération, on essaie de se souvenir du fait qu'on a une retenue dès qu'on dépasse ou égale 16. Je vous en pose une petite, pour que vous voyez un peu le résultat :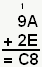







En détail, je commence par additionner A et E. D'après ma table d'addition, le résultat est 18. Donc je pose 8, et je retiens 1. J'ajoute ensuite 9 et 2, ce qui me donne B, auquel j'ajoute ma retenue, ça me donne C. J'ai donc mon résultat final : C8 !

Soustraction

Pour la soustraction, deux méthodes : soit vous la posez de façon "traditionnelle", soit vous la convertissez en addition d'opposé. Pour la méthode traditionnelle, rien de bien sorcier, c'est le même principe que d'habitude. Allons-y pour un exemple :









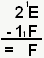
Pour le mode opératoire : je commence bien sûr par la droite : je fais donc E - F. Comme F est plus grand que E, je suis obligé de placer une retenue. Donc je dois faire 1E - F, qui me donne F (dans mon tableau d'addition, je cherche sur la ligne de F la case qui comporte le 1E et mon résultat est le nom de colonne !). Je passe à gauche, je n'oublie pas d'ajouter la retenue au chiffre du bas, donc 1 + 1, j'ai donc 2 - 2 qui me donne 0. Résultat de l'opération : F !

Multiplication

C'est toujours le même schéma que la multiplication décimale ou binaire. En dehors du fait qu'il faut utiliser les tables de multiplications hexadécimales; d'où l'intérêt du tableau donné plus haut. Posons donc une multiplication :







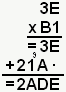
On commence par la droite : 1 x 3E... Ben c'est 3E. On passe au chiffre de gauche : on passe à la ligne, on laisse le blanc (ou le 0) traditionnel, et on attaque : B x E, d'après ma table, ça fait 9A. Je pose donc mon A, et je retiens 9. B x 3 nous donne 21, auquel il faudra que j'ajoute ma retenue de 9. Il ne me reste plus qu'à ajouter tout ça, de droite à gauche : E + 0 nous donne E, A + 3 nous donne D, 9 + 1 = A, et 2 + 0 nous donne 2. Résultat final : 2ADE !

Division

Alors la division... Euh... Comment dire ?

Eh bien disons qu'à moins de connaître par coeur votre table de multiplication hexadécimale (ce dont je doute ), vous ne pourrez arriver à rien. Vaut mieux repasser soit par le binaire, soit par le décimal !







C'est sur cette note pleine de réussite que se termine cette courte initiation à l'hexadécimal. Ne négligez pas cette base de calcul, elle vous servira grandement lors de la rédaction de vos programmes !