La Place des Développeurs Convertir vecteur en angle
Dans le cadre de mon projet Carwar, je cherche un moyen rapide de convertir un vecteur 2d (x,y) en angle (de 0 à N). J'ai déjà quelques idées, mais j'aimerai bien votre avis car la ruse sera surement plus utile que mes connaissances en géométrie.
Les valeurs de x,y peuvent être positives ou négatives, mais sont assez petite ; un octet signé (-128 à 127) serait largement suffisant.
Pour l'angle, dans l'idéal, j'aimerai récupérer des valeurs entre 0 et 63 (0° à 360°), mais de 0 à 7 pourrait être suffisant.
Évidement, toute opération mathématique complexe (division, racine carré), etc. est à proscrire. Par contre, j'ai des tables trigonométriques (sin, cos, etc.) à disposition.
Voici mon idée :
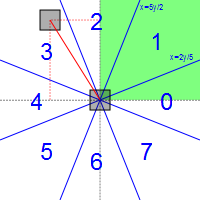
Sur le papier ça semble relativement rapide, mais le gros problème c'est que l'algorithme est difficilement applicable si on veut récupérer 16, 32 ou 64 valeurs d'angle.
Des idées, remarques, conseils ?
Les valeurs de x,y peuvent être positives ou négatives, mais sont assez petite ; un octet signé (-128 à 127) serait largement suffisant.
Pour l'angle, dans l'idéal, j'aimerai récupérer des valeurs entre 0 et 63 (0° à 360°), mais de 0 à 7 pourrait être suffisant.
Évidement, toute opération mathématique complexe (division, racine carré), etc. est à proscrire. Par contre, j'ai des tables trigonométriques (sin, cos, etc.) à disposition.
Voici mon idée :

- Prendre la valeur absolu de x et y (du coup, on travail uniquement dans le cadran haut-droite).
- Tester si |x| * 5 < |y| * 2. Si oui, sélection de l'angle A = 0, sinon passer au suivant.
- Tester si |x| * 2 < |y| * 5. Si oui, sélection de l'angle A = 1, sinon sélection de l'angle A = 2.
- Maintenant qu'on a notre angle de référence, on regarde les signes réels de x et y.
- Si x et y sont positif : l'angle A est déjà bon, on a fini.
- Si x est négatif et y positif : l'angle A = 4 - A.
- Si x et y sont négatifs : l'angle A = A + 4.
- Si x est positif et y négatif : l'angle A = 8 - A.
Sur le papier ça semble relativement rapide, mais le gros problème c'est que l'algorithme est difficilement applicable si on veut récupérer 16, 32 ou 64 valeurs d'angle.
Des idées, remarques, conseils ?
On est toujours ignorant avant de savoir.
Mais tu nous prépares quoi Aoineko ???
J'en sais fichtrement rien mais je m'en lèche les babines !!

@+
Guil'
J'en sais fichtrement rien mais je m'en lèche les babines !!

@+
Guil'
C'est typiquement le genre de situation ou une table précalculée est la meilleure solution.
Tu calcules tes angles en fonction d'une fourchette de valeurs de (x,y) et puis tu construis une table de référence.
Tu calcules tes angles en fonction d'une fourchette de valeurs de (x,y) et puis tu construis une table de référence.
MSX1: Daewoo DPC-200 / Yamaha CX5M
MSX2: Sony HB-F9P
MSXVR
Vidéo: V9990 (GFX-9)
Audio: MSX-Music (FM-PAC) / MSX-Audio (Audiowave) / OPL4 (Monster Sound FM Blaster) / OPNB (Neotron)
Quand je disais que x et y étaient petits, je pensai quand même à des valeurs pouvant aller jusque, disons, de -32 à +31. Il faudrait une table de 4096 entrées pour stocker tout ça. Ceci dit, si je me restreint de -16 à +15 et que je code mon angle sur 4 bits (0 à 15) ça fait que 512 octets.
Et puis, si mon vecteur est plus grand, je peux toujours diviser x et y par 2 jusqu'à ce qu'ils soient tous les 2 dans la fourchette.
Bon, adjuger pour la table pré-calculée.
Et puis, si mon vecteur est plus grand, je peux toujours diviser x et y par 2 jusqu'à ce qu'ils soient tous les 2 dans la fourchette.
Bon, adjuger pour la table pré-calculée.

On est toujours ignorant avant de savoir.
Répondre
Vous n'êtes pas autorisé à écrire dans cette catégorie

