La Place des Développeurs Jeux Infocom Version MSX2
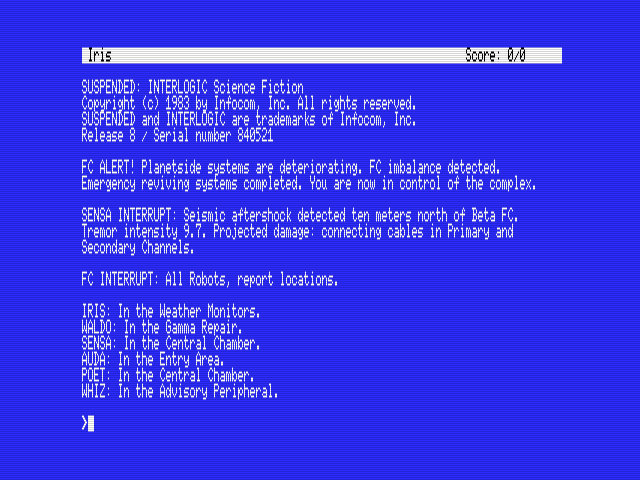
J'ai profité de mon temps libre, pour commencer la conversion de Suspended, un magnifique jeu d'Infocom, jamais sorti sur MSX.
Voici l'état d'avancement: (je pense que tout y est, mais je dois encore tester...)
Deadline.zip
Suspended.zip
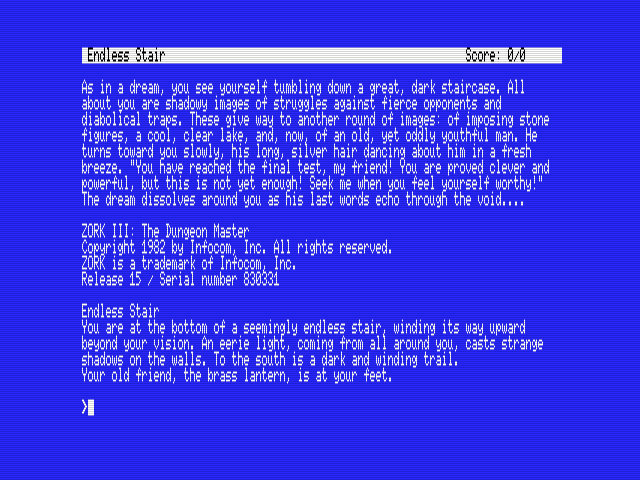
Zork.zip
Edité par
Sector28
Le 06/05/2020 à 15h20
Voici l'état d'avancement: (je pense que tout y est, mais je dois encore tester...)
Deadline.zip
Suspended.zip
Zork.zip
Edité par
Sector28
Le 06/05/2020 à 15h20
Un endomorphisme u d'un espace vectoriel E est trigonalisable si et seulement si E est la somme directe des sous-espaces caractéristiques de u, c'est-à-dire si et seulement s'il existe une base de E formée de vecteurs propres généralisés de u. Cette caractérisation rejoint celle donnée à l'aide du polynôme caractéristique, qui doit être scindé pour que l'endomorphisme soit trigonalisable.
Un endomorphisme u d'un espace vectoriel E est trigonalisable si et seulement si E est la somme directe des sous-espaces caractéristiques de u, c'est-à-dire si et seulement s'il existe une base de E formée de vecteurs propres généralisés de u. Cette caractérisation rejoint celle donnée à l'aide du polynôme caractéristique, qui doit être scindé pour que l'endomorphisme soit trigonalisable.
Il n'y a pas de version MSX officielle pour Zork I, II ou III.
Le manuel et la carte de Suspended se trouvent dans l'archive ZIP.
Il faut imprimer la carte et utiliser, par exemple, des jetons de différentes couleurs pour marquer l'emplacement des six robots sur la carte. Sinon, c'est impossible à jouer.
Le manuel et la carte de Suspended se trouvent dans l'archive ZIP.
Il faut imprimer la carte et utiliser, par exemple, des jetons de différentes couleurs pour marquer l'emplacement des six robots sur la carte. Sinon, c'est impossible à jouer.
Un endomorphisme u d'un espace vectoriel E est trigonalisable si et seulement si E est la somme directe des sous-espaces caractéristiques de u, c'est-à-dire si et seulement s'il existe une base de E formée de vecteurs propres généralisés de u. Cette caractérisation rejoint celle donnée à l'aide du polynôme caractéristique, qui doit être scindé pour que l'endomorphisme soit trigonalisable.
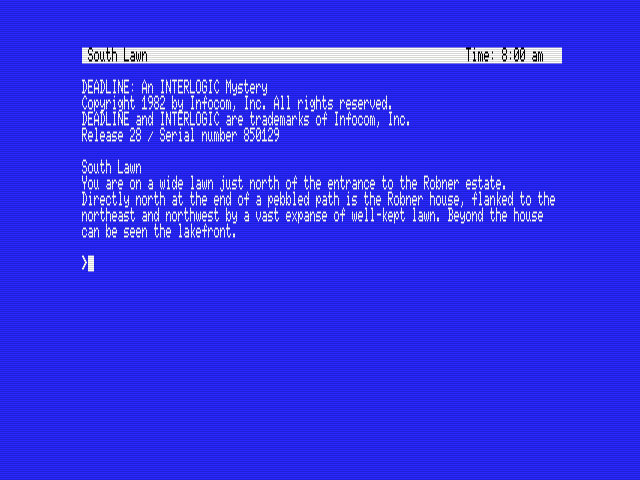
Voici la conversion de Deadline, je n'ai pas encore tout vérifié..
Deadline.zip
J'ai terminé le jeu Suspended, et tout a l'air ok.
Deadline.zip
J'ai terminé le jeu Suspended, et tout a l'air ok.
Un endomorphisme u d'un espace vectoriel E est trigonalisable si et seulement si E est la somme directe des sous-espaces caractéristiques de u, c'est-à-dire si et seulement s'il existe une base de E formée de vecteurs propres généralisés de u. Cette caractérisation rejoint celle donnée à l'aide du polynôme caractéristique, qui doit être scindé pour que l'endomorphisme soit trigonalisable.
Il s'agit d'une disquette double-face formatée en simple-face.
Certains MSX2 n'acceptent pas le double-face, comme le vg8235 de Philips.
Je commence la conversion de la trilogie Spellbreaker ...
Certains MSX2 n'acceptent pas le double-face, comme le vg8235 de Philips.
Je commence la conversion de la trilogie Spellbreaker ...
Un endomorphisme u d'un espace vectoriel E est trigonalisable si et seulement si E est la somme directe des sous-espaces caractéristiques de u, c'est-à-dire si et seulement s'il existe une base de E formée de vecteurs propres généralisés de u. Cette caractérisation rejoint celle donnée à l'aide du polynôme caractéristique, qui doit être scindé pour que l'endomorphisme soit trigonalisable.
j'ai fait une version 720k de Zork avec un loader
on peux y rajouter tes autres jeux tant qu'il y a de la place
Zork Menu.dsk
on peux y rajouter tes autres jeux tant qu'il y a de la place
Zork Menu.dsk
Joli ! 
Un endomorphisme u d'un espace vectoriel E est trigonalisable si et seulement si E est la somme directe des sous-espaces caractéristiques de u, c'est-à-dire si et seulement s'il existe une base de E formée de vecteurs propres généralisés de u. Cette caractérisation rejoint celle donnée à l'aide du polynôme caractéristique, qui doit être scindé pour que l'endomorphisme soit trigonalisable.
- J'utilise IDA pour désassembler le programme cp/m (rétro-ingénierie).
- Je modifie le source obtenu pour qu'il fonctionne correctement sur MSX.
- J'assemble mon programme avec ZMAC.
Voilà
- Je modifie le source obtenu pour qu'il fonctionne correctement sur MSX.
- J'assemble mon programme avec ZMAC.
Voilà
Un endomorphisme u d'un espace vectoriel E est trigonalisable si et seulement si E est la somme directe des sous-espaces caractéristiques de u, c'est-à-dire si et seulement s'il existe une base de E formée de vecteurs propres généralisés de u. Cette caractérisation rejoint celle donnée à l'aide du polynôme caractéristique, qui doit être scindé pour que l'endomorphisme soit trigonalisable.
Sector28_3 :
J'ai profité de mon temps libre, pour commencer la conversion de Suspended, un magnifique jeu d'Infocom, jamais sorti sur MSX.
Covinou :
Et moi alors 
Quand on a les compétences et les connaissances
manqué simplement le temps 
Franck :
Mais alors 
... J'aurais jamais fini la liste :'(
... J'aurais jamais fini la liste :'( Ça dépend... Si t' arrive a suivre le rythme de Sector28_3
Edité par
TurboSEB
Le 07/05/2020 à 06h49
MSX 1&2 + Moniteurs+divers (environ 0.70Tonnes)
Répondre
Vous n'êtes pas autorisé à écrire dans cette catégorie