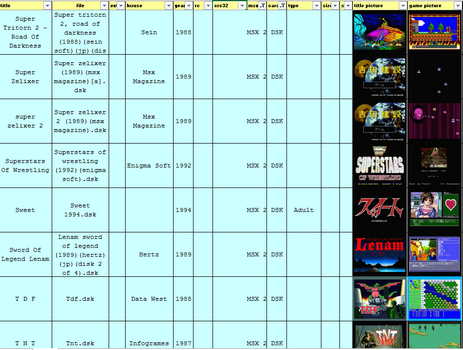
Salle de Jeux Liste des jeux MSX: le retour
Après des années, et plus de 2460 jeux testés, François Pignon a bien avancé sur sa Tour Eiffel en allumettes , voici une version qui intègre les jeux MSX2.
Il me manque encore pas mal de jeux des années 2000, je suis en train de les explorer.
Explications: il n'y a pas de score mais seulement des jeux qui m'ont plu et d'autres moins, soit pour des raisons techniques, de jouabilité ou tout simplement parce que je n'y ai rien compris (par exemple pour les jeux en japonais).
Le fichier est un fichier Libre Office, pour ceux qui l'ont, pour les autres je vous invite à l'installer, c'est gratuit
JEUX MSX1 MSX2 25 Avril 2020.ods
Il me manque encore pas mal de jeux des années 2000, je suis en train de les explorer.
Explications: il n'y a pas de score mais seulement des jeux qui m'ont plu et d'autres moins, soit pour des raisons techniques, de jouabilité ou tout simplement parce que je n'y ai rien compris (par exemple pour les jeux en japonais).
Le fichier est un fichier Libre Office, pour ceux qui l'ont, pour les autres je vous invite à l'installer, c'est gratuit

JEUX MSX1 MSX2 25 Avril 2020.ods
Super alors ! 
Franchement pour un besoin personnel, ça ne sert strictement à rien de payer pour Office, Libre Office le fait aussi bien pour 99% des utilisateurs, et gratuitement en plus
Si vous souhaitez me signaler des erreurs, n'hésitez pas à me contacter en MP.
En complément, 3 sites indispensables pour les listes de logiciels:
Bien entendu, Generation-MSX, la MSX Database, très complète mais qui ne semble pas comporter les derniers jeux:
https://www.generation-msx.nl/search/result?q=uwasa
Ensuite la base de données de Konamito, très complète, sur laquelle on peut télécharger les jeux, et à jour très rapidement (les jeux d'Eric ont été très vite intégrés).
https://www.msxgamesworld.com/index.php
Enfin D-MSX, extrêmement complète mais en espagnol:
https://dmsx.es/index.php

Franchement pour un besoin personnel, ça ne sert strictement à rien de payer pour Office, Libre Office le fait aussi bien pour 99% des utilisateurs, et gratuitement en plus

Si vous souhaitez me signaler des erreurs, n'hésitez pas à me contacter en MP.
En complément, 3 sites indispensables pour les listes de logiciels:
Bien entendu, Generation-MSX, la MSX Database, très complète mais qui ne semble pas comporter les derniers jeux:
https://www.generation-msx.nl/search/result?q=uwasa
Ensuite la base de données de Konamito, très complète, sur laquelle on peut télécharger les jeux, et à jour très rapidement (les jeux d'Eric ont été très vite intégrés).
https://www.msxgamesworld.com/index.php
Enfin D-MSX, extrêmement complète mais en espagnol:
https://dmsx.es/index.php
Zork, un des 1001 jeux à faire avant de mourir, classé "BOF" 
Selon moi, le jeu de réflexion le plus difficile sur MSX, j'ai beaucoup souffert à l'époque pour le terminer..
"It is pitch black, you are likely to be eaten by a goonies.."
Randar I et II sont d'excellents jeux (BOF->BIEN), tout comme les deux Hurry Fox.

Selon moi, le jeu de réflexion le plus difficile sur MSX, j'ai beaucoup souffert à l'époque pour le terminer..

"It is pitch black, you are likely to be eaten by a goonies.."
Randar I et II sont d'excellents jeux (BOF->BIEN), tout comme les deux Hurry Fox.
DONALD TRUMP IS FAST APPROACHING
NEMESIS ! RETURN IMMEDIATELY !
Répondre
Vous n'êtes pas autorisé à écrire dans cette catégorie



 un grand
un grand