Maire-adjoint


Inscrit le : 02/10/2009 à 19h33
Messages: 2571
Reprise du message précédent
Quand on fait ESC dans le menu, on revient au menu Disc Station les copains

Maire-adjoint


Inscrit le : 02/10/2009 à 19h41
Messages: 11164
petit curieux , je m'en suis aperçu aussi mais pas réussi a le bloquer pour l'instant

Maire-adjoint


Inscrit le : 02/10/2009 à 22h54
Messages: 3345
Quelle idée de toucher partout aussi

Maire-adjoint


Inscrit le : 02/10/2009 à 19h41
Messages: 11164
la solution immédiate : retirer le cabochon de la touche ESC

Maire-adjoint


Inscrit le : 02/10/2009 à 22h54
Messages: 3345
Ne lui donne pas de mauvaise idée, il ne faut pas qu'il abuse du bricolage

Maire-adjoint


Inscrit le : 02/10/2009 à 19h41
Messages: 11164
c'est vrai que j'avais oublié ce détail

Maire-adjoint


Inscrit le : 02/10/2009 à 19h33
Messages: 2571
J'ai dessoudé la touche ESC et mon MSX ne démarre plus...

Villageois

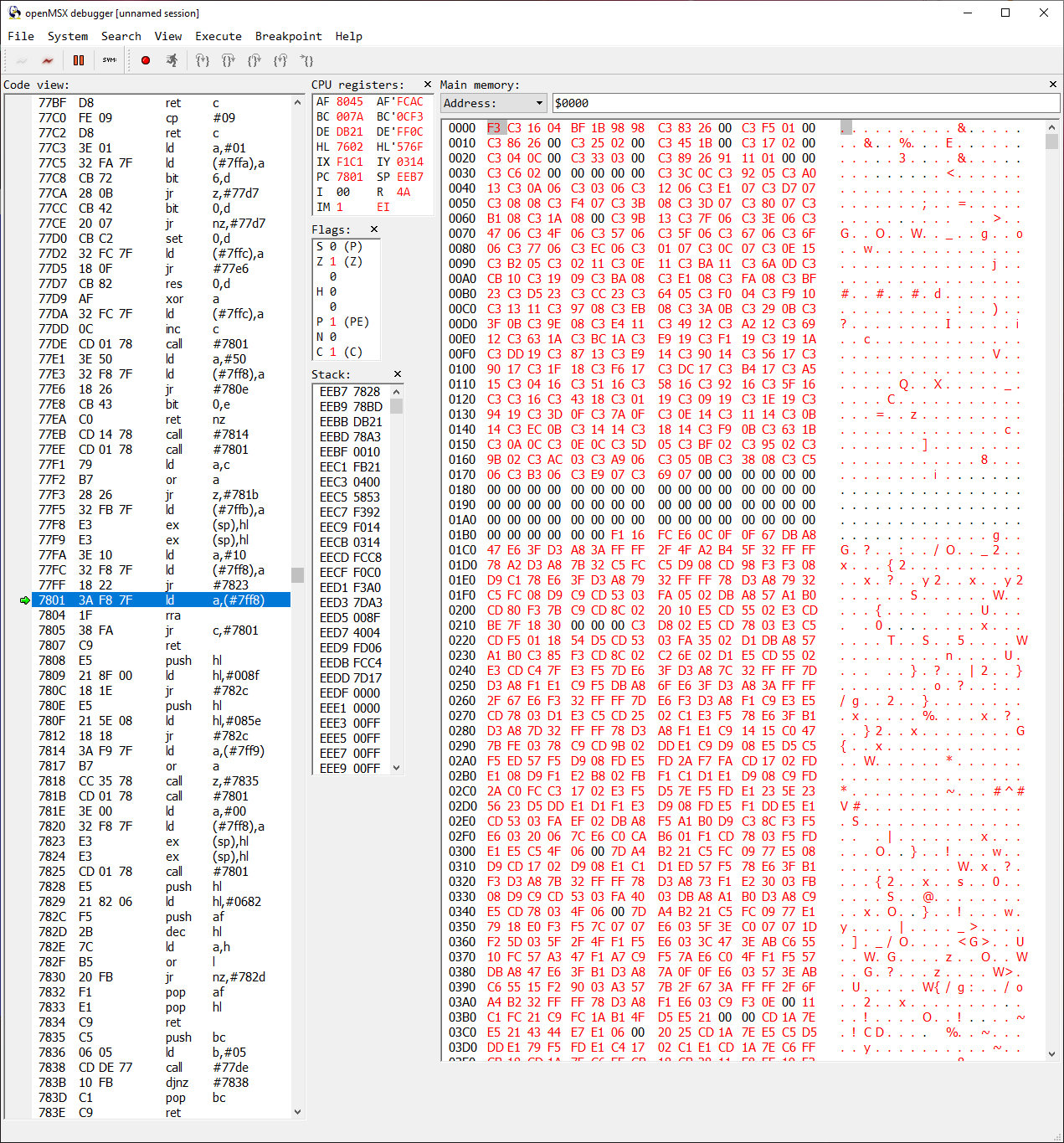
Pour visualiser la RAM en temps réel, utilise openMSX, son débogueur est de loin meilleur que celui de blueMSX.
DONALD TRUMP IS FAST APPROACHING
NEMESIS ! RETURN IMMEDIATELY !
Maire-adjoint


Inscrit le : 02/10/2009 à 19h41
Messages: 11164
comment tu fait pour parametrer la taille des fenetres dans ce debugger
Villageois

Il faut les décrocher en cliquant sur le titre, changer la taille et les raccrocher.
Edité par
Sector28
Le 17/06/2020 à 13h46
DONALD TRUMP IS FAST APPROACHING
NEMESIS ! RETURN IMMEDIATELY !
Maire-adjoint


Inscrit le : 02/10/2009 à 19h41
Messages: 11164
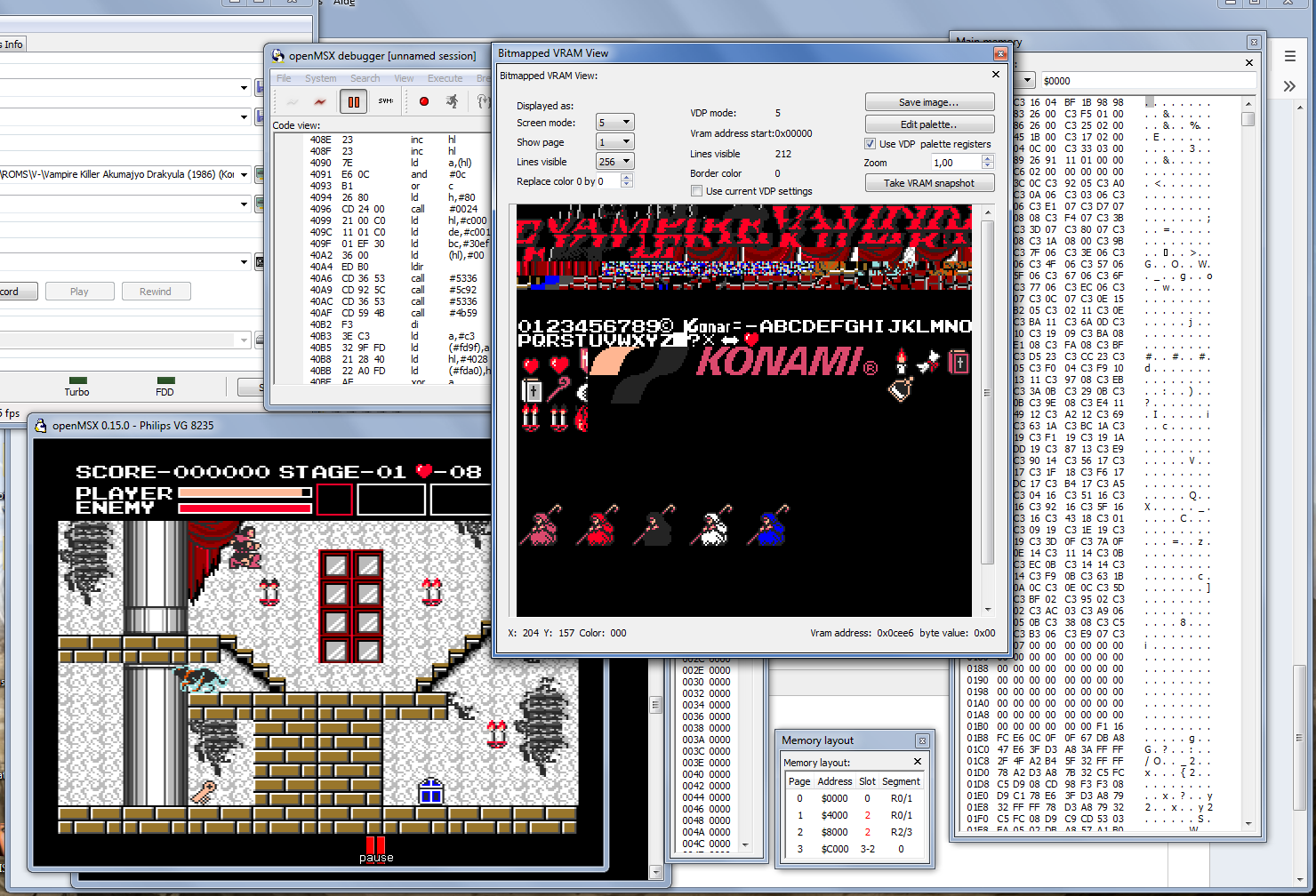
je n'arrive pas a rétrécir la fenêtre Code View dans la fenêtre principale
du coup je travaille en multi-fenêtres et je commence a maitriser
Villageois

Rétrécir en hauteur ou en largeur ?
Essaie de fermer toutes les autres fenêtres, rétrécis la fenêtre principale, puis rouvre les fenêtres.
DONALD TRUMP IS FAST APPROACHING
NEMESIS ! RETURN IMMEDIATELY !
Maire-adjoint


Inscrit le : 02/10/2009 à 19h41
Messages: 11164
en fait je n'arrive pas a rétrécir Code View en largeur comme toi
j'y arrive seulement quand les fenêtres sont séparées
tu travaille avec quel systéme ?
moi c'est Windows 7
Villageois

J'ai windows 10.
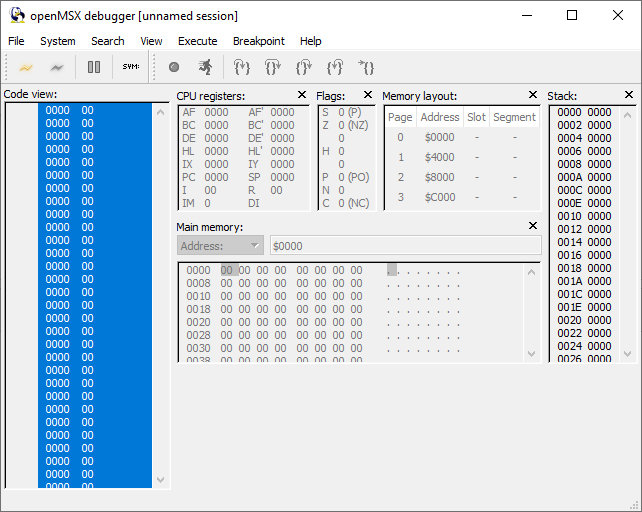
Dans l’éditeur registre tu vas dans HKEY_CURRENT_USER\Software\openMSX
et tu supprime la clé "debugger" et tu relance le debugger
ça doit ressembler à ceci:
DONALD TRUMP IS FAST APPROACHING
NEMESIS ! RETURN IMMEDIATELY !
Maire-adjoint


Inscrit le : 02/10/2009 à 19h41
Messages: 11164
impeccable ton truc

Répondre
Vous n'êtes pas autorisé à écrire dans cette catégorie












