Se repérer dans un plan
Le cours qui suit a pour but de vous familiariser avec la notion de plan et de coordonnées, ce qui vous permettra de bien saisir ce qu'il faut faire lorsque vous passerez à la programmation pour réaliser vos affichages à l'écran. Bonne lecture !
Vous avez sans doute tous déjà joué à la bataille navale... Votre adversaire et vous placez vos bateaux horizontalement ou verticalement sur un quadrillage, marqué horizontalement pas des nombres et verticalement par des lettres. Lorsque vous souhaitez torpiller une position sur le quadrillage, vous annoncez la case du quadrillage correspondante (en général d'abord la lettre, puis le chiffre, genre C8). Eh bien mine de rien, ce petit jeu vous représente exactement la technique qui est utilisée pour se repérer dans un plan.

Ah oui, c'est vrai, je ne vous ai pas dit ce qu'était un plan . Eh bien, vous pouvez vous imaginer qu'un plan c'est comme une une feuille blanche très fine qui s'étendrait à l'infini. Revenons à nos moutons donc : comment faire pour se repérer sur un plan ? Eh bien en adoptant le système de la bataille navale, c'est à dire en créant un genre de quadrillage de ce plan. Sur ce quadrillage, il nous faudra être capables de nous repérer, et donc d'utiliser un système de coordonnées. Comme pour la bataille navale donc, sauf qu'au lieu de lettres, on utilisera aussi des nombres.
. Eh bien, vous pouvez vous imaginer qu'un plan c'est comme une une feuille blanche très fine qui s'étendrait à l'infini. Revenons à nos moutons donc : comment faire pour se repérer sur un plan ? Eh bien en adoptant le système de la bataille navale, c'est à dire en créant un genre de quadrillage de ce plan. Sur ce quadrillage, il nous faudra être capables de nous repérer, et donc d'utiliser un système de coordonnées. Comme pour la bataille navale donc, sauf qu'au lieu de lettres, on utilisera aussi des nombres.
Avant d'aller plus loin, il est capital de savoir que si les coordonnées sont des bien nombres, il faut forcément un début... Ben oui, si je mets un point à la coordonnée verticale 1, il faut bien pouvoir calculer ce 1 par rapport à quelque chose ! On admettra donc que ce "début" est le point de coordonnées 0 horizontalement et 0 verticalement. On appelle ce point l'origine. D'ailleurs, tant qu'on est à faire du vocabulaire, il vous faudra retenir que les 2 coordonnées utilisées pour se repérer sont nommées abscisse et ordonnée (nous rentrerons plus tard dans le détail). Ceci étant, ce n'est pas encore suffisant pour pouvoir placer des points sur mon quadrillage ! La preuve, regardez ce représentation de plan avec son origine (on place un point nommé O... comme origine, qu'est-ce que c'est... original ).
).

Là réside toute la subtilité : tout d'abord, on va faire passer par notre point origine deux droites perpendiculaires (ou orthogonales). Pour rappel deux droites perpendiculaires forment un angle droit (90°). On obtient donc un dessin comme ceci :
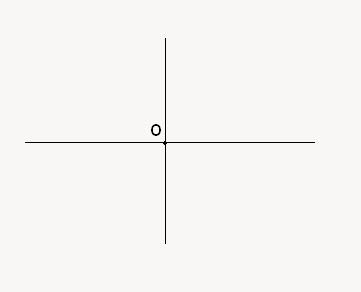
Oui, en passant, je ne sais pas si vous avez placé vos droites perpendiculaires comme moi, mais je me suis permis de redresser le tout, histoire d'avoir une verticale et une horizontale... (après tout c'est la représentation classique ). Ainsi nous avons les directions à suivre pour nos abscisses et ordonnées. L'abscisse sera la coordonnée sur l'axe horizontal, l'ordonnée celle sur l'axe vertical. Alors maintenant on a certes la direction, mais pas le sens ! Vous verrez que tout sera différent en fonction du sens (par exemple, lorsque vous programmerez frénétiquement votre MSX favori, vous verrez que les abscisses croissantes vont à droite et les ordonnées croissantes vont vers le bas). Ici, nous utiliserons le sens "habituel" des cours de mathématiques :
). Ainsi nous avons les directions à suivre pour nos abscisses et ordonnées. L'abscisse sera la coordonnée sur l'axe horizontal, l'ordonnée celle sur l'axe vertical. Alors maintenant on a certes la direction, mais pas le sens ! Vous verrez que tout sera différent en fonction du sens (par exemple, lorsque vous programmerez frénétiquement votre MSX favori, vous verrez que les abscisses croissantes vont à droite et les ordonnées croissantes vont vers le bas). Ici, nous utiliserons le sens "habituel" des cours de mathématiques :
- abscisses croissantes vers la droite
- ordonnées croissantes vers le haut
On a notre direction, notre sens, il nous reste juste à graduer notre plan. Dans l'absolu, on peut prendre les divisions que l'on souhaite sur chacun des axes, mais en pratique, il est bien plus commode de travailler avec des graduations identiques sur les deux axes. Un tel plan est dit normé. A présent pour se repérer sur les axes, il suffit de savoir que suivant le sens, les abscisses et ordonnées sont positives après le point d'origine. Et d'ailleurs, on appellera dorénavant l'axe horizontal axe des abscisses, le vertical axe des ordonnées.
Voilà le résultat de notre plan avec toutes les informations nécessaires pour placer des points :
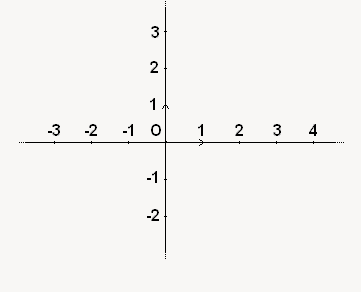
On dit alors que le plan est pourvu d'un repère orthonormé (directions orthogonales, et repère normé, d'où le joli nom du repère ). Vous remarquerez que nos axes délimitent le plan en 4 parties : ces parties sont appelées quadrants. Ils sont numérotés de 1 à 4, et s'organisent comme dans le schéma suivant :
). Vous remarquerez que nos axes délimitent le plan en 4 parties : ces parties sont appelées quadrants. Ils sont numérotés de 1 à 4, et s'organisent comme dans le schéma suivant :
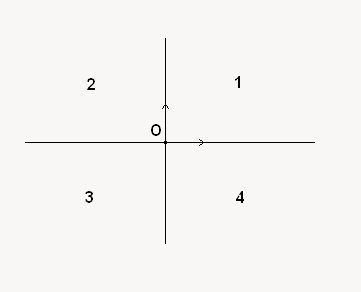
Le quadrant 1 est celui des abscisses et ordonnées positives.
Le quadrant 2 est celui des abscisses négatives et ordonnées positives.
Le quadrant 3 est celui des abscisses et ordonnées négatives.
Le quadrant 4 est celui des abscisses positives et ordonnées négatives.
A présent, on va pouvoir mettre plein de choses sur notre plan, grâce aux coordonnées !
Afin de se faciliter la tâche, on va employer les deux systèmes utilisés habituellement pour notifier des coordonnées d'un élément du plan. Tout d'abord, on utilisera des lettres pour symboliser l'abscisse et l'ordonnée. X sera l'abscisse, Y l'ordonnée.
La première solution est la suivante : pour donner les coordonnées d'un élément A, on écrira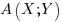 .
.
La deuxième méthode est plus... verticale , mais vous verrez qu'elle nous sera utile pour réaliser des calculs. On utilise cette notation :
, mais vous verrez qu'elle nous sera utile pour réaliser des calculs. On utilise cette notation :
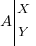
Suivant les cas, je pourrai alterner de l'une à l'autre notation, c'est juste pour que vous ne soyez pas trop perdus !
Le premier des éléments qu'on pourra positionner grâce à notre repère, c'est le point. C'est très facile : pour obtenir les coordonnées d'un point que vous positionnez sur le plan, il suffit de tirer deux traits à partir de ce point : un vers l'axe des abscisses, l'autre vers l'axe des ordonnées. Cette technique s'appelle la projection sur un axe. Il ne vous reste plus qu'à lire votre graduation pour trouver les coordonnées de votre point. Facile, non ? Ci-dessous un exemple, on va placer un point A quelconque sur notre plan :
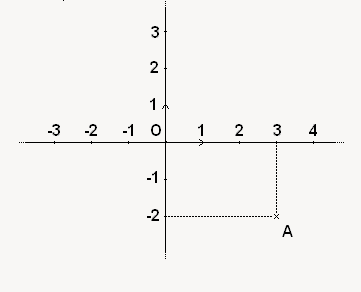
Grâce à mes projections, je trouve que l'abscisse de mon point est 3, et l'ordonnée -2. J'ai donc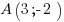 .
.
De la même manière, si vous avez un point à placer dont vous connaissez les coordonnées, il vous suffit de suivre votre graduation sur les deux axes pour placer le point. Imaginons que j'aie le point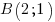 à placer :
à placer :
1ère étape : je cale mon abscisse. Pour cela, je trace une droite verticale qui coupe l'axe des abscisses à l'abscisse souhaitée :
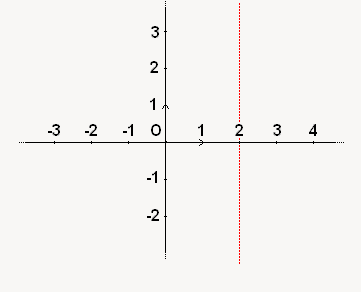
2ème étape : je cale mon ordonnée. Je trace cette fois une droite horizontale qui coupe l'axe des ordonnées à l'ordonnée souhaitée :
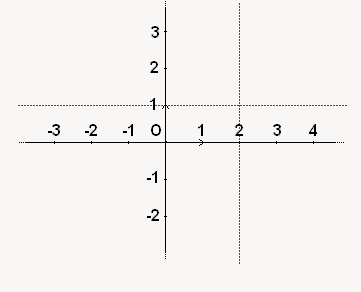
Le point que je place est ainsi à l'intersection de ces deux droites !
Pour calculer une distance entre deux points, il existe une formule se servant de leurs coordonnées. Je ne vais pas vous faire une démonstration pour ça (pour ceux que ça intéresse, ça utilise le théorème de Pythagore ), je vais vous la donner en "brut".
), je vais vous la donner en "brut".
On va prendre deux points A et B, et leurs coordonnées respectives. On pose donc :
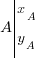 et
et 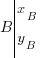 ou
ou 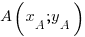 et
et 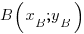
La formule pour calculer la distance est la suivante :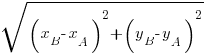
En détaillant : vous faites d'abord la différence entre les abscisses (peu importe l'ordre d'ailleurs ici), puis vous les mettez au carré.
Ah la la, vous avez déjà oublié les puissances du cours sur le binaire ? Mettre un nombre au carré, c'est le multiplier par lui-même !!
Ensuite, vous faites la différence entre les ordonnées, que vous mettez également au carré.
Vous ajoutez les deux nombres ainsi trouvés, et vous prenez la racine carré de ce nombre. La racine carrée, c'est l'exact contraire de la mise au carré d'un nombre. C'est trouver le nombre qui, une fois multiplié par lui-même, nous donne le résultat sous le symbole de la racine carrée. Par exemple,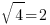 , parce que
, parce que 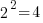 . Au pire, vous avez des calculatrices qui feront très bien ça pour vous !
. Au pire, vous avez des calculatrices qui feront très bien ça pour vous ! 
Un petit exemple pour illustrer ça ? Allez, on va prendre les points A et B de coordonnées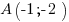 et
et 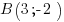
Je commence par faire la différence des deux abscisses : j'ai donc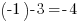 . Je mets ce nombre au carré :
. Je mets ce nombre au carré : 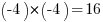
Je fais la même chose pour les ordonnées : j'ai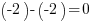 . Et 0 au carré... ça donne 0 ! J'ajoute ces deux nombres, j'obtiens donc 16.
. Et 0 au carré... ça donne 0 ! J'ajoute ces deux nombres, j'obtiens donc 16.
Il ne me reste plus qu'à prendre la racine carrée de 16. Ça tombe bien, c'est un carré facile qui tombe pile poil sur un entier (quel exemple bien choisi )!
)! 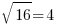
Voilà, la distance entre mes deux points est donc de 4 ! Regardez la représentation suivante, vous verrez effectivement que la distance qui sépare nos deux points est bien de 4 unités !
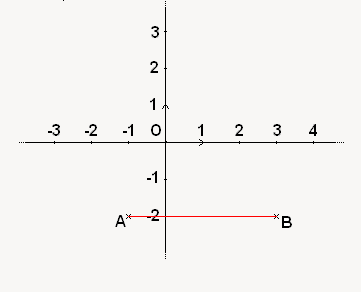
Comme maintenant on sait placer des points, il va nous être relativement facile de placer d'autres éléments. Mais avant tout, on va voir un peu de jargon mathématique, pour réussir à faire les différences entre les éléments dont on parlera par la suite !
Une droite est une ligne droite (d'où son nom, heureusement que je suis là n'est-ce pas ), de longueur infinie, d'épaisseur nulle. Dans un plan, on représente facilement une droite en utilisant deux points. Il n'existe qu'une seule droite pouvant passer par deux points distincts !
), de longueur infinie, d'épaisseur nulle. Dans un plan, on représente facilement une droite en utilisant deux points. Il n'existe qu'une seule droite pouvant passer par deux points distincts !
Évidemment . On ne va pas représenter TOUTE la droite, seulement la partie qui nous intéresse ! Mais avant de visualiser cela sur un repère, on va indiquer la notation adéquate: pour définir une droite dans un énoncé, on met son nom entre parenthèses (ou alors les deux points qui la caractérisent). Bien sûr, vous n'appellerez pas votre droite Roger ou Michel, il est de coutume de prendre la lettre D (comme droite, ils se foulent beaucoup les matheux
. On ne va pas représenter TOUTE la droite, seulement la partie qui nous intéresse ! Mais avant de visualiser cela sur un repère, on va indiquer la notation adéquate: pour définir une droite dans un énoncé, on met son nom entre parenthèses (ou alors les deux points qui la caractérisent). Bien sûr, vous n'appellerez pas votre droite Roger ou Michel, il est de coutume de prendre la lettre D (comme droite, ils se foulent beaucoup les matheux  ).
).
J'aurai donc la droite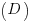 , ou si elle passe par les points A et B par exemple
, ou si elle passe par les points A et B par exemple 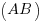 .
.
Pour la figurer sur un repère, si vous la placez "au hasard", pensez à mettre son petit nom à l'une de ses extrémités, comme sur la figure suivante :
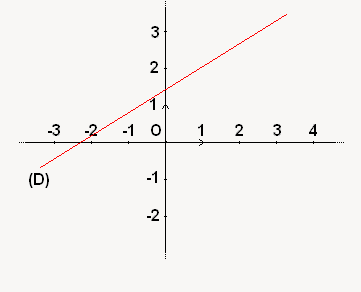
Par contre, si vous la placez en utilisant deux points existants (ici on a pris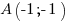 et
et 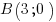 ) veillez bien à la faire dépasser de part et d'autre des points, comme dans l'illustration ci-dessous :
) veillez bien à la faire dépasser de part et d'autre des points, comme dans l'illustration ci-dessous :
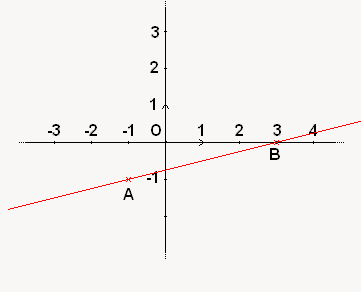
On aura l'occasion de reparler des droites par la suite, mais pour l'instant vous en savez suffisamment !
Un segment, comme son nom le laisse supposer, est un morceau de droite, de longueur finie et d'épaisseur nulle, qui est défini par deux points qui sont ses extrémités.
Pour parler d'un segment, on utilise les crochets, dans lesquels on place les noms des extrémités. Par exemple, pour un segment d'extrémités A et B, je note donc![[AB] [AB]](/images/maths/math_982_db96b1e83cd7acd5004a95bfe69909ba.png) .
.
Pour sa représentation, je vais reprendre les mêmes points que pour la droite qu'on a vu ci-dessus :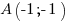 et
et 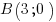
Cette fois, contrairement à la droite, vous ne devez pas dépasser des extrémités ! Voilà comment on le représente :
Si vous voulez vous amuser à calculer sa longueur (au segment hein, à quoi pensiez-vous ? ), je vous renvoie quelques lignes plus haut, tout vous a été expliqué !
), je vous renvoie quelques lignes plus haut, tout vous a été expliqué ! 
Ahhh, le vecteur ! Un outil très puissant dans les repères, il va grandement nous servir ! Par contre, il va falloir se retrousser un peu les manches pour bien cerner son principe.
Un vecteur est défini par trois choses :
En gros, c'est un peu comme un segment, mais orienté, et sans le principe des extrémités. Du coup, pour représenter un vecteur dans un plan vous avez une infinité de possibilités !
En fait tout vient de sa "vraie" définition initiale : on part d'un parallélogramme et...
Alors... Le parallélogramme, c'est une figure géométrique à 4 côtés, avec la particularité d'avoir ses côtés parallèles deux à deux. Avant que vous ne le demandiez, on dit que deux droites sont parallèles si et seulement si elles ne se coupent en aucun point ! Allez, je vais vous faire un petit dessin de parallélogramme. On va l'appeler ABCD :
Donc sur mon illustration, les droites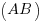 et
et 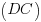 sont parallèles, de même pour les droites
sont parallèles, de même pour les droites 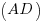 et
et 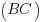 .
.
Je reprends donc après cet aparté subtil : lorsqu'on part d'un parallélogramme, on se rend compte de plusieurs choses. Déjà le fait qu'il y ait parallélisme (donc des directions identiques). Ensuite, vous pouvez vous amuser à mesurer les côtés, vous verrez à votre grande stupéfaction que les côtés parallèles ont la même longueur. Eh bien nous y sommes : si on oriente comme il faut les segments figurant les côtés, on trouve deux représentants d'un même vecteur !
Pour la notation, on surplombe le nom du vecteur (ou du couple de points qui le représente) d'une flèche, comme ceci :
Pour sa représentation graphique, sur notre repère, il suffit de mettre une flèche indiquant son sens ! Voici un exemple d'un vecteur totalement mis au hasard dans un repère orthonormé :
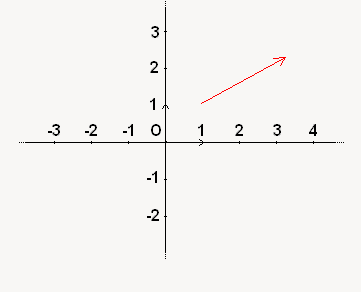
Ce qui est encore plus magique avec un vecteur, c'est qu'il peut avoir des coordonnées ! On peut donc le représenter facilement dans un repère.
Par exemple, je vais prendre le vecteur suivant :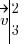
Sans indication complémentaire (on verra plus tard le cas où il y en a, je vous rassure ), il vous suffit de prendre un point quelconque de votre repère (pour l'exemple présent je choisis arbitrairement le point de coordonnées
), il vous suffit de prendre un point quelconque de votre repère (pour l'exemple présent je choisis arbitrairement le point de coordonnées 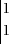 , mais libre à vous d'en choisir un autre à votre convenance
, mais libre à vous d'en choisir un autre à votre convenance  ).
).
A partir de ce point, j'ajoute mes coordonnées de vecteur : j'avance donc de 2 sur l'axe des abscisses, et de 3 sur l'axe des ordonnées. Et voilà, le résultat est ci-dessous !
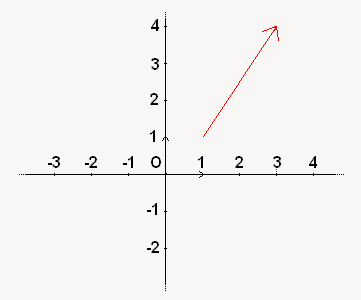
Après, il peut vous être imposé de représenter un vecteur à partir d'un point donné, mais le principe reste identique : vous n'avez qu'à ajouter les coordonnées du vecteur à celles du point imposé pour en trouver la deuxième extrémité !
C'est un peu grâce à cela qu'on peut s'apercevoir qu'il existe autant de possibilités de représenter un vecteur dans un repère que de points dans ce repère, donc... un fort joli paquet !
Lorsque vous avez un couple de points avec leurs coordonnées respectives, vous pouvez également parvenir à calculer l'abscisse et l'ordonnée d'un vecteur correspondant. Ce n'est pas sorcier, mais il faut bien être attentif au sens du vecteur pour ne pas se tromper dans le calcul des coordonnées. Rien de tel qu'un petit exemple pour se faire la main :
Prenons les points suivants :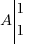 et
et 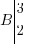
On va immédiatement les positionner dans un repère :
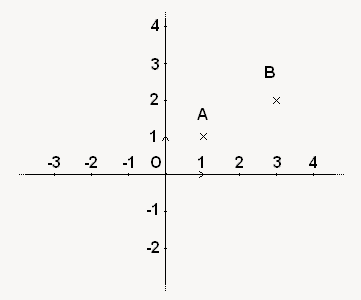
De là, on voit bien que j'ai deux possibilités : soit j'ai le vecteur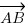 , avec le sens de A vers B, soit le vecteur
, avec le sens de A vers B, soit le vecteur 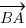 avec le sens de B vers A ! On se décide donc pour s'occuper du vecteur
avec le sens de B vers A ! On se décide donc pour s'occuper du vecteur 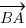 . Alors soyez attentifs : les coordonnées d'un vecteur sont les différences entre les coordonnées de son point d'arrivée et son point de départ.
. Alors soyez attentifs : les coordonnées d'un vecteur sont les différences entre les coordonnées de son point d'arrivée et son point de départ.
Pour mon exemple, j'aurai donc l'abscisse de mon vecteur qui sera égale à l'abscisse de B (point d'arrivée) moins l'abscisse de A (point de départ), et pareil pour son ordonnée. En posant le calcul, vous obtenez
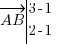 , soit
, soit 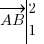
A l'inverse, si j'avais étudié le vecteur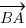 , le calcul des coordonnées aurait été le suivant :
, le calcul des coordonnées aurait été le suivant :
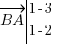 , soit
, soit 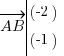 .
.
Tiens c'est amusant, vous avez remarqué ? Les coordonnées de ce vecteur sont les opposées de celle du vecteur précédent ! Eh bien oui, lorsqu'on a un vecteur de même direction et de même norme, si son sens change, alors on prend les coordonnées opposées !
Nous allons aborder ici pas mal de règles différentes à propos du calcul sur les vecteurs, vous verrez là que c'est un outil réellement puissant (niveau mathématique, évidemment ).
).
Somme de vecteurs
Les vecteurs étant des outils géométriques assez particuliers, il est possible de les ajouter. Prenons un petit exemple, avec sa représentation sur un repère. Ici nous aurons 3 points :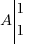 ,
, 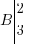 B et
B et 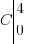 . Mon but est d'ajouter
. Mon but est d'ajouter 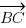 à
à 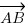 .
.
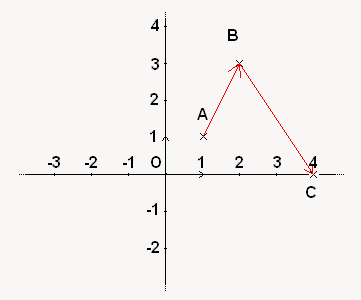
On va essayer d'imaginer un point qui se déplace. Il part du point A vers le point B (il suit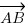 ), puis du point B vers le point C (il suit
), puis du point B vers le point C (il suit 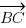 ). J'aurai donc effectué au final le trajet de A vers C. Ajouter deux vecteurs, c'est en fait ajouter leurs coordonnés respectives ! Je vais calculer les coordonnées de mes 2 vecteurs :
). J'aurai donc effectué au final le trajet de A vers C. Ajouter deux vecteurs, c'est en fait ajouter leurs coordonnés respectives ! Je vais calculer les coordonnées de mes 2 vecteurs :
D'abord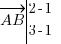 soit
soit 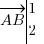 .
.
Ensuite,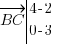 soit
soit 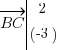 .
.
J'ajoute maitenant les coordonnées ainsi trouvées : j'ai 1+2=3 en abscisse, et 2-3=-1 en ordonnée. Calculons à présent les coordonnées du vecteur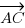 . On a :
. On a :
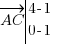 soit
soit 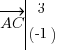 .
.
Ca alors, c'est les coordonnées qu'on a trouvé en additionnant les deux vecteurs ! N'est-ce pas magique ? Grâce à cet exemple, non seulement vous savez ajouter deux vecteurs mais vous avez la définition de ce qu'on appelle la relation de Chasles.
C'est une égalité qui vous permet de décomposer un vecteur en une somme de vecteurs. En fait pour tout vecteur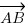 et pour tout point M quelconque du plan, on a l'égalité suivante qui est TOUJOURS vérifiée :
et pour tout point M quelconque du plan, on a l'égalité suivante qui est TOUJOURS vérifiée :
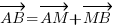 .
.
Sinon en passant, comme vous savez maintenant additionner deux vecteurs, vous savez aussi en pratique les soustraire. Ben oui ! Soustraire (souvenez-vous) c'est ajouter l'opposé ! Et les coordonnées de l'opposé d'un vecteur comme on l'a vu pus haut sont les opposées des coordonnées de ce vecteur !
Pour tout vecteur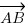 , on peut noter
, on peut noter 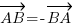
Le vecteur nul
Le vecteur nul est un vecteur qui a 0 en abscisse comme en ordonnée. Reprenons rapidement la dernière ligne précédente :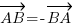 . Si je fais donc
. Si je fais donc 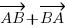 , j'obtiens des coordonnées nulles (ou le vecteur
, j'obtiens des coordonnées nulles (ou le vecteur 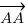 si j'utilise la relation de Chasles, celui-ci aura aussi des coordonnées nulles, voir plus haut). Il est représenté par un 0 surmonté de la flèche typique des vecteurs :
si j'utilise la relation de Chasles, celui-ci aura aussi des coordonnées nulles, voir plus haut). Il est représenté par un 0 surmonté de la flèche typique des vecteurs : 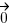 .
.
Multiplication d'un nombre par un vecteur
Forcément, si vous pouvez additionner des vecteurs, vous comprendrez bien qu'on peut aussi les multiplier, mais ATTENTION, pas entre eux, uniquement par un nombre !
Si je fais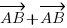 , j'ai bien
, j'ai bien 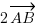 . Pour avoir les coordonnées, il suffit alors de multiplier celles du vecteur d'origine par le nombre en question. Si j'avais ici par exemple
. Pour avoir les coordonnées, il suffit alors de multiplier celles du vecteur d'origine par le nombre en question. Si j'avais ici par exemple 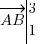 , j'aurai
, j'aurai 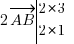 soit
soit 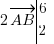 .
.
Vecteurs colinéaires
Euh... Si J'avoue qu'il y a pas mal de vocabulaire à assimiler, mais là, le principe est assez aisé à comprendre. On dit de deux vecteurs qu'ils sont colinéaires s'ils ont la même direction, tout simplement.
J'avoue qu'il y a pas mal de vocabulaire à assimiler, mais là, le principe est assez aisé à comprendre. On dit de deux vecteurs qu'ils sont colinéaires s'ils ont la même direction, tout simplement.
Par exemple, si je prends les points suivants :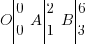 . Les plus fûtés d'entre vous remarqueront qu'on a
. Les plus fûtés d'entre vous remarqueront qu'on a 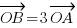 . Eh bien ceux-là ont tout compris (et les autres l'apprennent maintenant
. Eh bien ceux-là ont tout compris (et les autres l'apprennent maintenant  ) : pour que deux vecteurs soient colinéaires, il suffit qu'il existe un coéfficient quelconque qui fait qu'on puisse retrouver les coordonnées de l'un par rapport à l'autre. En formule "mathématique", on dira que deux vecteurs
) : pour que deux vecteurs soient colinéaires, il suffit qu'il existe un coéfficient quelconque qui fait qu'on puisse retrouver les coordonnées de l'un par rapport à l'autre. En formule "mathématique", on dira que deux vecteurs 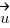 et
et 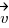 sont colinéaires si et seulement si il existe un nombre k (oui on l'appelle k comme on aurait pu l'appeler Robert ou T, mais bon... je m'égare) tel que
sont colinéaires si et seulement si il existe un nombre k (oui on l'appelle k comme on aurait pu l'appeler Robert ou T, mais bon... je m'égare) tel que 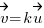 .
.
Je vous mets quand même les points de mon exemple, pour que vous voyez que ces points sont bien sur la même direction (ici c'est un cas simple vu que les points sont effectivement alignés, mais vous pourriez très bien avoir des vecteurs de directions parallèles). Voilà le dessin :
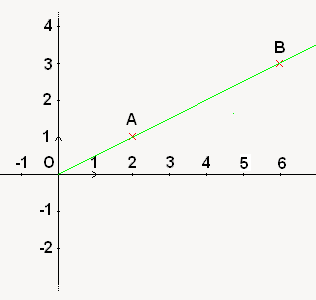
Après, quand vous avez les coordonnées de deux vecteurs, il y a une méthode infaillible pour déterminer si ceux-ci sont colinéaires ou pas. On va reprendre nos vecteurs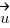 et
et 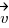 . Ecrivons leurs coordonnées :
. Ecrivons leurs coordonnées : 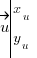 et
et 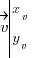 .
.
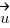 et
et 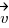 sont colinéaires si et seulement si
sont colinéaires si et seulement si 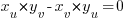 . La preuve avec notre exemple (je vous épargne les calculs des coordonnées, normalement vous savez faire maintenant :
. La preuve avec notre exemple (je vous épargne les calculs des coordonnées, normalement vous savez faire maintenant : ) : j'ai
) : j'ai 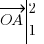 et
et 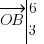 . J'applique ma nouvelle formule : je dois donc calculer 2*3 - 1*6, donc 6-6, donc 0. Mes vecteurs sont bien colinéaires !!
. J'applique ma nouvelle formule : je dois donc calculer 2*3 - 1*6, donc 6-6, donc 0. Mes vecteurs sont bien colinéaires !!
Cette partie est importante pour ce qui suivra prochainement, n'hésitez donc pas à faire et refaire des essais pour bien acquérir la technique de vérification de colinéarité.
Vecteurs orthogonaux
La dernière chose à savoir, c'est que grâce aux coordonnées, vous pouvez savoir si deux vecteurs ont leurs directions qui sont orthogonales (pour rappel, qui forment un angle droit). Cette fois, il faut appliquer la formule suivante (je garde les vecteurs et coordonnées du paragraphe précédent) :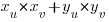 . Si le résultat est nul, vos vecteurs ont leurs directions orthogonales. Un exemple concret ? On prend les points suivants :
. Si le résultat est nul, vos vecteurs ont leurs directions orthogonales. Un exemple concret ? On prend les points suivants : 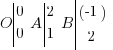
Voici le dessin de tout ça, et même à l'oeil nu vous pouvez voir qu'effectivement, l'angle entre les directions de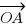 et
et 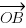 est droit.
est droit.
Je fais à présent le calcul pour confirmer tout ça :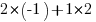 , soit
, soit 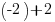 , soit
, soit 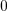 .
.
Voilà qui démontre que la formule de calcul est bonne !
Grâce aux vecteurs, nous allons être en mesure de définir une équation (rappelez-vous, une expression contenant un signe "=") pour représenter une droite. Le but est de pouvoir représenter une droite comme un ensemble de points, dont on calcule l'ordonnée en fonction de l'abscisse ! Ce qui est plus qu'utile lorsqu'on souhaite par exemple représenter une trajectoire linéaire.
Comme son nom l'indique, on peut déterminer un vecteur qui indique la direction d'une droite. Il suffit de prendre deux points (bien placés pour faciliter les calculs) sur la représentation d'une droite, et vous aurez les coordonnées de ce vecteur directeur. Reprenons une représentation de droite déjà vue précédemment :

Cette droite passe par les points A et B, on peut donc dire que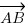 est un vecteur directeur de cette droite. Ses coordonnées sont les suivantes :
est un vecteur directeur de cette droite. Ses coordonnées sont les suivantes :
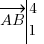
Pour déterminer l'équation d'une droite, vous n'avez besoin que des coordonnées de deux points de celle-ci. On va reprendre l'exemple du dessus avec les points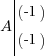 et
et 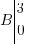
On va partir du principe qu'il y a sur la droite un point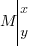 .
.
Comme on l'a dit plus haut, le fait que M soit sur la droite implique que les différents vecteurs qu'on peut former avec ces 3 points soient colinéaires. On va donc prendre un vecteur dont on peut déterminer les coordonnées (au hasard le vecteur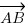 qui est le vecteur directeur), puis un vecteur quelconque, soit
qui est le vecteur directeur), puis un vecteur quelconque, soit 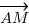 , soit
, soit 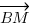 . Par commodité pour les calculs qui vont suivre, je choisis
. Par commodité pour les calculs qui vont suivre, je choisis 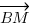 .
.
J'ai donc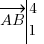 et
et 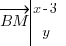 .
.
Ces 2 vecteurs étant par définition colinéaires, je peux appliquer ma formule qui permet de vérifier la colinéarité, et ainsi trouver l'égalité suivante, qui est vérifiée !
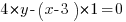 , ce qui équivaut à
, ce qui équivaut à 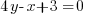 , ou encore, après avoir tout rangé comme il faut :
, ou encore, après avoir tout rangé comme il faut : 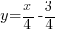
Et voilà, j'ai mon équation de droite ! Les coordonnées de tous les points de la droite vérifieront cette équation. Si vous remplacez les x et y de l'équation respectivement par l'abscisse et l'ordonnée d'un point de la droite, vous aurez toujours une égalité vérifiée. Vous ne me croyez pas ? Eh bien testons avec les deux points connus A et B !
Pour A, je remplace les x et y de l'équation par les "bonnes" coordonnées :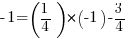 , ce qui me donne
, ce qui me donne 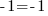 : c'est vérifié !
: c'est vérifié !
Idem pour B :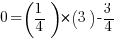 ce qui me donne
ce qui me donne 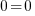 , c'est vérifié aussi !
, c'est vérifié aussi !
L'équation de droite peut ainsi vous servir à trouver un point sur la droite si vous ne connaissez que son abscisse ou son ordonnée. Si je cherche par exemple le point de la droite qui a une abscisse nulle, il me suffit de remplacer x par 0 dans l'équation, et je trouve directement l'ordonnée (je vous dispense des calculs, mais si vous les faites, vous trouverez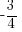 .
.
D'ailleurs, l'ordonnée de ce point particulier d'abscisse 0 sur une droite est appelé l'ordonnée à l'origine !
La majorité des équations de droites (les cas particuliers seront abordés plus bas, ne vous inquiétez pas ) sera de la forme
) sera de la forme 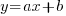 avec a et b, deux nombres quelconques. Le nombre a est appelé coefficient directeur, et b, on l'a déjà vu, c'est l'ordonnée à l'origine. Si vous avez un vecteur directeur d'une droite, et les coordonnées d'un point de cette droite, il est assez facile de déterminer l'équation de celle-ci. Le calcul du coefficient directeur se fait en faisant la division de l'ordonnée du vecteur directeur par son abscisse. Si j'applique ce calcul avec mon exemple précédent, j'avais le vecteur directeur
avec a et b, deux nombres quelconques. Le nombre a est appelé coefficient directeur, et b, on l'a déjà vu, c'est l'ordonnée à l'origine. Si vous avez un vecteur directeur d'une droite, et les coordonnées d'un point de cette droite, il est assez facile de déterminer l'équation de celle-ci. Le calcul du coefficient directeur se fait en faisant la division de l'ordonnée du vecteur directeur par son abscisse. Si j'applique ce calcul avec mon exemple précédent, j'avais le vecteur directeur 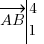 : mon coefficient directeur est donc bien
: mon coefficient directeur est donc bien 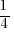 (la preuve, regardez à nouveau l'équation qu'on a trouvé précédemment !).
(la preuve, regardez à nouveau l'équation qu'on a trouvé précédemment !).
A partir de là, je sais que mon équation de droite sera de la forme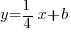 . Après il me reste à prendre les coordonnées d'un point connu de la droite, et de remplacer dans cette dernière équation x et y par les coordonnées du point. Si je prends le point B, je trouve donc :
. Après il me reste à prendre les coordonnées d'un point connu de la droite, et de remplacer dans cette dernière équation x et y par les coordonnées du point. Si je prends le point B, je trouve donc :
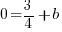 . Je résous l'équation, je trouve
. Je résous l'équation, je trouve 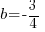 . J'ai donc mon coefficient directeur et mon ordonnée à l'origine : je peux donc écrire mon équation de droite qui est bien
. J'ai donc mon coefficient directeur et mon ordonnée à l'origine : je peux donc écrire mon équation de droite qui est bien 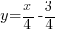
Comme dit au paragraphe du dessus, il y a certaines droites qui ont des équations pour le moins particulières. Ces droites sont les parallèles aux axes de mon repère ! Eh oui, regardez un peu le dessin suivant, ou je fais passer des droites respectivement parallèle à l'axe des abscisses par le point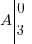 , et à l'axe des ordonnées par le point
, et à l'axe des ordonnées par le point 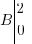 :
:
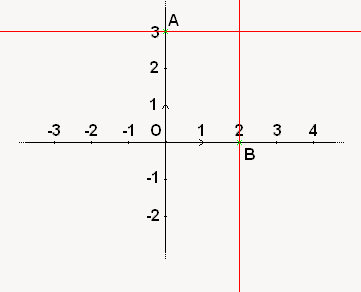
Pour la droite qui passe par le point A, on remarque que quelle que soit l'abscisse du point de la droite, l'ordonnée sera toujours de 3. L'équation est ici on ne peut plus simple :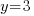 . Eh oui, l'ordonnée ne se calcule pas ici en fonction de l'abscisse, vu qu'elle est constante ! En conclusion, toute droite parallèle à l'axe des abscisses sera de la forme
. Eh oui, l'ordonnée ne se calcule pas ici en fonction de l'abscisse, vu qu'elle est constante ! En conclusion, toute droite parallèle à l'axe des abscisses sera de la forme 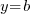 , avec b un nombre quelconque.
, avec b un nombre quelconque.
Pour celle qui passe par le point B, c'est pareil, à ceci près que c'est cette fois l'abscisse qui reste constante. Pour mon exemple, l'équation est donc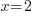 . Donc au final toute droite parallèle à l'axe des ordonnées sera de la forme
. Donc au final toute droite parallèle à l'axe des ordonnées sera de la forme 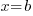 , avec b un nombre quelconque.
, avec b un nombre quelconque.
Enfin, il y a une droite à l'équation un peu particulière :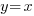 . Sur cette droite (qui passe par l'origine), tous les points ont leurs abscisses et ordonnées égales. En voici la représentation :
. Sur cette droite (qui passe par l'origine), tous les points ont leurs abscisses et ordonnées égales. En voici la représentation :
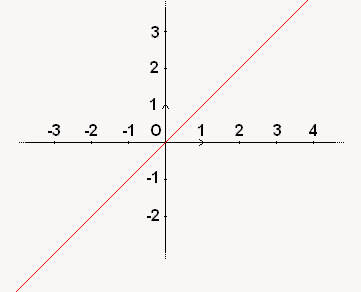
Voilà qui conclut ce chapitre sur les équations de droites !
Il aurait été possible d'aller encore plus loin, mais je vais arrêter là ce tutoriel sur les repères. Il est cependant fort probable que vous les retrouviez dans un prochain tuto mathématique, donc ne vous endormez pas sur les acquis.
En fait, pour ceux qui veulent aller plus loin, sachez qu'on peut aussi trouver des équations pour toute une floppée de courbes et formes diverses, mais là on entre dans une méthode un peu plus pointue, qui s'appelle l'étude de fonctions (qui se voit lors des années de première et terminale scientifique), et qui couvre vraiment un champ de possibilités très large. Vous en savez a priori pour le moment assez, vous savez placer des points dans un repère et déterminer des équations de droites, vous avez ainsi un petit bagage intéressant pour aborder sereinement la programmation côté graphique de vos MSX chéris !
Le repère orthonormé (ou orthonormal)
Touché, coulé !
Vous avez sans doute tous déjà joué à la bataille navale... Votre adversaire et vous placez vos bateaux horizontalement ou verticalement sur un quadrillage, marqué horizontalement pas des nombres et verticalement par des lettres. Lorsque vous souhaitez torpiller une position sur le quadrillage, vous annoncez la case du quadrillage correspondante (en général d'abord la lettre, puis le chiffre, genre C8). Eh bien mine de rien, ce petit jeu vous représente exactement la technique qui est utilisée pour se repérer dans un plan.

Ah oui, c'est vrai, je ne vous ai pas dit ce qu'était un plan
 . Eh bien, vous pouvez vous imaginer qu'un plan c'est comme une une feuille blanche très fine qui s'étendrait à l'infini. Revenons à nos moutons donc : comment faire pour se repérer sur un plan ? Eh bien en adoptant le système de la bataille navale, c'est à dire en créant un genre de quadrillage de ce plan. Sur ce quadrillage, il nous faudra être capables de nous repérer, et donc d'utiliser un système de coordonnées. Comme pour la bataille navale donc, sauf qu'au lieu de lettres, on utilisera aussi des nombres.
. Eh bien, vous pouvez vous imaginer qu'un plan c'est comme une une feuille blanche très fine qui s'étendrait à l'infini. Revenons à nos moutons donc : comment faire pour se repérer sur un plan ? Eh bien en adoptant le système de la bataille navale, c'est à dire en créant un genre de quadrillage de ce plan. Sur ce quadrillage, il nous faudra être capables de nous repérer, et donc d'utiliser un système de coordonnées. Comme pour la bataille navale donc, sauf qu'au lieu de lettres, on utilisera aussi des nombres.Mise en place d'un repère du plan
Avant d'aller plus loin, il est capital de savoir que si les coordonnées sont des bien nombres, il faut forcément un début... Ben oui, si je mets un point à la coordonnée verticale 1, il faut bien pouvoir calculer ce 1 par rapport à quelque chose ! On admettra donc que ce "début" est le point de coordonnées 0 horizontalement et 0 verticalement. On appelle ce point l'origine. D'ailleurs, tant qu'on est à faire du vocabulaire, il vous faudra retenir que les 2 coordonnées utilisées pour se repérer sont nommées abscisse et ordonnée (nous rentrerons plus tard dans le détail). Ceci étant, ce n'est pas encore suffisant pour pouvoir placer des points sur mon quadrillage ! La preuve, regardez ce représentation de plan avec son origine (on place un point nommé O... comme origine, qu'est-ce que c'est... original
 ).
).
Là réside toute la subtilité : tout d'abord, on va faire passer par notre point origine deux droites perpendiculaires (ou orthogonales). Pour rappel deux droites perpendiculaires forment un angle droit (90°). On obtient donc un dessin comme ceci :

Oui, en passant, je ne sais pas si vous avez placé vos droites perpendiculaires comme moi, mais je me suis permis de redresser le tout, histoire d'avoir une verticale et une horizontale... (après tout c'est la représentation classique
 ). Ainsi nous avons les directions à suivre pour nos abscisses et ordonnées. L'abscisse sera la coordonnée sur l'axe horizontal, l'ordonnée celle sur l'axe vertical. Alors maintenant on a certes la direction, mais pas le sens ! Vous verrez que tout sera différent en fonction du sens (par exemple, lorsque vous programmerez frénétiquement votre MSX favori, vous verrez que les abscisses croissantes vont à droite et les ordonnées croissantes vont vers le bas). Ici, nous utiliserons le sens "habituel" des cours de mathématiques :
). Ainsi nous avons les directions à suivre pour nos abscisses et ordonnées. L'abscisse sera la coordonnée sur l'axe horizontal, l'ordonnée celle sur l'axe vertical. Alors maintenant on a certes la direction, mais pas le sens ! Vous verrez que tout sera différent en fonction du sens (par exemple, lorsque vous programmerez frénétiquement votre MSX favori, vous verrez que les abscisses croissantes vont à droite et les ordonnées croissantes vont vers le bas). Ici, nous utiliserons le sens "habituel" des cours de mathématiques :- abscisses croissantes vers la droite
- ordonnées croissantes vers le haut
On a notre direction, notre sens, il nous reste juste à graduer notre plan. Dans l'absolu, on peut prendre les divisions que l'on souhaite sur chacun des axes, mais en pratique, il est bien plus commode de travailler avec des graduations identiques sur les deux axes. Un tel plan est dit normé. A présent pour se repérer sur les axes, il suffit de savoir que suivant le sens, les abscisses et ordonnées sont positives après le point d'origine. Et d'ailleurs, on appellera dorénavant l'axe horizontal axe des abscisses, le vertical axe des ordonnées.
Voilà le résultat de notre plan avec toutes les informations nécessaires pour placer des points :

On dit alors que le plan est pourvu d'un repère orthonormé (directions orthogonales, et repère normé, d'où le joli nom du repère
 ). Vous remarquerez que nos axes délimitent le plan en 4 parties : ces parties sont appelées quadrants. Ils sont numérotés de 1 à 4, et s'organisent comme dans le schéma suivant :
). Vous remarquerez que nos axes délimitent le plan en 4 parties : ces parties sont appelées quadrants. Ils sont numérotés de 1 à 4, et s'organisent comme dans le schéma suivant :
Le quadrant 1 est celui des abscisses et ordonnées positives.
Le quadrant 2 est celui des abscisses négatives et ordonnées positives.
Le quadrant 3 est celui des abscisses et ordonnées négatives.
Le quadrant 4 est celui des abscisses positives et ordonnées négatives.
A présent, on va pouvoir mettre plein de choses sur notre plan, grâce aux coordonnées !
Les points sur un repère
Conventions d'écriture
Afin de se faciliter la tâche, on va employer les deux systèmes utilisés habituellement pour notifier des coordonnées d'un élément du plan. Tout d'abord, on utilisera des lettres pour symboliser l'abscisse et l'ordonnée. X sera l'abscisse, Y l'ordonnée.
La première solution est la suivante : pour donner les coordonnées d'un élément A, on écrira
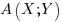 .
.La deuxième méthode est plus... verticale
 , mais vous verrez qu'elle nous sera utile pour réaliser des calculs. On utilise cette notation :
, mais vous verrez qu'elle nous sera utile pour réaliser des calculs. On utilise cette notation :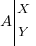
Suivant les cas, je pourrai alterner de l'une à l'autre notation, c'est juste pour que vous ne soyez pas trop perdus !

Identifier ou placer un point
Le premier des éléments qu'on pourra positionner grâce à notre repère, c'est le point. C'est très facile : pour obtenir les coordonnées d'un point que vous positionnez sur le plan, il suffit de tirer deux traits à partir de ce point : un vers l'axe des abscisses, l'autre vers l'axe des ordonnées. Cette technique s'appelle la projection sur un axe. Il ne vous reste plus qu'à lire votre graduation pour trouver les coordonnées de votre point. Facile, non ? Ci-dessous un exemple, on va placer un point A quelconque sur notre plan :

Grâce à mes projections, je trouve que l'abscisse de mon point est 3, et l'ordonnée -2. J'ai donc
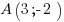 .
.De la même manière, si vous avez un point à placer dont vous connaissez les coordonnées, il vous suffit de suivre votre graduation sur les deux axes pour placer le point. Imaginons que j'aie le point
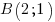 à placer :
à placer :1ère étape : je cale mon abscisse. Pour cela, je trace une droite verticale qui coupe l'axe des abscisses à l'abscisse souhaitée :

2ème étape : je cale mon ordonnée. Je trace cette fois une droite horizontale qui coupe l'axe des ordonnées à l'ordonnée souhaitée :

Le point que je place est ainsi à l'intersection de ces deux droites !
Calculer une distance entre 2 points
Pour calculer une distance entre deux points, il existe une formule se servant de leurs coordonnées. Je ne vais pas vous faire une démonstration pour ça (pour ceux que ça intéresse, ça utilise le théorème de Pythagore
 ), je vais vous la donner en "brut".
), je vais vous la donner en "brut".On va prendre deux points A et B, et leurs coordonnées respectives. On pose donc :
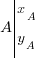 et
et 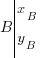 ou
ou 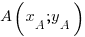 et
et 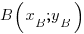
La formule pour calculer la distance est la suivante :
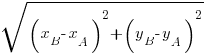
En détaillant : vous faites d'abord la différence entre les abscisses (peu importe l'ordre d'ailleurs ici), puis vous les mettez au carré.
Ah la la, vous avez déjà oublié les puissances du cours sur le binaire ? Mettre un nombre au carré, c'est le multiplier par lui-même !!
Ensuite, vous faites la différence entre les ordonnées, que vous mettez également au carré.
Vous ajoutez les deux nombres ainsi trouvés, et vous prenez la racine carré de ce nombre. La racine carrée, c'est l'exact contraire de la mise au carré d'un nombre. C'est trouver le nombre qui, une fois multiplié par lui-même, nous donne le résultat sous le symbole de la racine carrée. Par exemple,
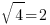 , parce que
, parce que 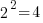 . Au pire, vous avez des calculatrices qui feront très bien ça pour vous !
. Au pire, vous avez des calculatrices qui feront très bien ça pour vous ! 
Un petit exemple pour illustrer ça ? Allez, on va prendre les points A et B de coordonnées
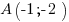 et
et 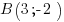
Je commence par faire la différence des deux abscisses : j'ai donc
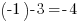 . Je mets ce nombre au carré :
. Je mets ce nombre au carré : 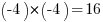
Je fais la même chose pour les ordonnées : j'ai
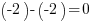 . Et 0 au carré... ça donne 0 ! J'ajoute ces deux nombres, j'obtiens donc 16.
. Et 0 au carré... ça donne 0 ! J'ajoute ces deux nombres, j'obtiens donc 16.Il ne me reste plus qu'à prendre la racine carrée de 16. Ça tombe bien, c'est un carré facile qui tombe pile poil sur un entier (quel exemple bien choisi
 )!
)! 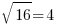
Voilà, la distance entre mes deux points est donc de 4 ! Regardez la représentation suivante, vous verrez effectivement que la distance qui sépare nos deux points est bien de 4 unités !

Droites, segments et vecteurs
Comme maintenant on sait placer des points, il va nous être relativement facile de placer d'autres éléments. Mais avant tout, on va voir un peu de jargon mathématique, pour réussir à faire les différences entre les éléments dont on parlera par la suite !
Définitions, notations et représentations
Droite
Une droite est une ligne droite (d'où son nom, heureusement que je suis là n'est-ce pas
 ), de longueur infinie, d'épaisseur nulle. Dans un plan, on représente facilement une droite en utilisant deux points. Il n'existe qu'une seule droite pouvant passer par deux points distincts !
), de longueur infinie, d'épaisseur nulle. Dans un plan, on représente facilement une droite en utilisant deux points. Il n'existe qu'une seule droite pouvant passer par deux points distincts !Évidemment
 . On ne va pas représenter TOUTE la droite, seulement la partie qui nous intéresse ! Mais avant de visualiser cela sur un repère, on va indiquer la notation adéquate: pour définir une droite dans un énoncé, on met son nom entre parenthèses (ou alors les deux points qui la caractérisent). Bien sûr, vous n'appellerez pas votre droite Roger ou Michel, il est de coutume de prendre la lettre D (comme droite, ils se foulent beaucoup les matheux
. On ne va pas représenter TOUTE la droite, seulement la partie qui nous intéresse ! Mais avant de visualiser cela sur un repère, on va indiquer la notation adéquate: pour définir une droite dans un énoncé, on met son nom entre parenthèses (ou alors les deux points qui la caractérisent). Bien sûr, vous n'appellerez pas votre droite Roger ou Michel, il est de coutume de prendre la lettre D (comme droite, ils se foulent beaucoup les matheux  ).
).J'aurai donc la droite
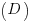 , ou si elle passe par les points A et B par exemple
, ou si elle passe par les points A et B par exemple 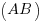 .
.Pour la figurer sur un repère, si vous la placez "au hasard", pensez à mettre son petit nom à l'une de ses extrémités, comme sur la figure suivante :
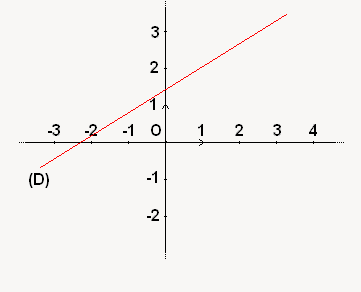
Par contre, si vous la placez en utilisant deux points existants (ici on a pris
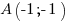 et
et 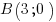 ) veillez bien à la faire dépasser de part et d'autre des points, comme dans l'illustration ci-dessous :
) veillez bien à la faire dépasser de part et d'autre des points, comme dans l'illustration ci-dessous :
On aura l'occasion de reparler des droites par la suite, mais pour l'instant vous en savez suffisamment !

Segment
Un segment, comme son nom le laisse supposer, est un morceau de droite, de longueur finie et d'épaisseur nulle, qui est défini par deux points qui sont ses extrémités.
Pour parler d'un segment, on utilise les crochets, dans lesquels on place les noms des extrémités. Par exemple, pour un segment d'extrémités A et B, je note donc
![[AB] [AB]](/images/maths/math_982_db96b1e83cd7acd5004a95bfe69909ba.png) .
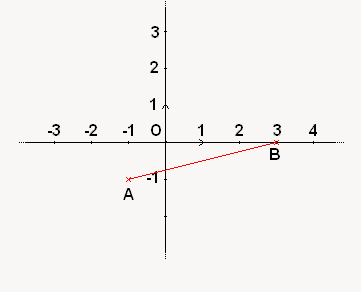
.Pour sa représentation, je vais reprendre les mêmes points que pour la droite qu'on a vu ci-dessus :
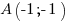 et
et 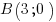
Cette fois, contrairement à la droite, vous ne devez pas dépasser des extrémités ! Voilà comment on le représente :

Si vous voulez vous amuser à calculer sa longueur (au segment hein, à quoi pensiez-vous ?
 ), je vous renvoie quelques lignes plus haut, tout vous a été expliqué !
), je vous renvoie quelques lignes plus haut, tout vous a été expliqué ! 
Vecteur
Définition
Ahhh, le vecteur ! Un outil très puissant dans les repères, il va grandement nous servir ! Par contre, il va falloir se retrousser un peu les manches pour bien cerner son principe.
Un vecteur est défini par trois choses :
- Sa direction
- Son sens
- Sa longueur (appelée norme)
En gros, c'est un peu comme un segment, mais orienté, et sans le principe des extrémités. Du coup, pour représenter un vecteur dans un plan vous avez une infinité de possibilités !
En fait tout vient de sa "vraie" définition initiale : on part d'un parallélogramme et...
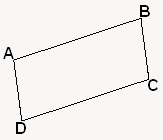
Alors... Le parallélogramme, c'est une figure géométrique à 4 côtés, avec la particularité d'avoir ses côtés parallèles deux à deux. Avant que vous ne le demandiez, on dit que deux droites sont parallèles si et seulement si elles ne se coupent en aucun point ! Allez, je vais vous faire un petit dessin de parallélogramme. On va l'appeler ABCD :

Donc sur mon illustration, les droites
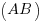 et
et 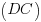 sont parallèles, de même pour les droites
sont parallèles, de même pour les droites 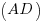 et
et 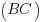 .
.Je reprends donc après cet aparté subtil : lorsqu'on part d'un parallélogramme, on se rend compte de plusieurs choses. Déjà le fait qu'il y ait parallélisme (donc des directions identiques). Ensuite, vous pouvez vous amuser à mesurer les côtés, vous verrez à votre grande stupéfaction que les côtés parallèles ont la même longueur. Eh bien nous y sommes : si on oriente comme il faut les segments figurant les côtés, on trouve deux représentants d'un même vecteur !
Pour la notation, on surplombe le nom du vecteur (ou du couple de points qui le représente) d'une flèche, comme ceci :
- Pour un vecteur nommé v :
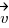
- Pour son représentant par exemple avec le couple de points A et B :
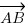
Pour sa représentation graphique, sur notre repère, il suffit de mettre une flèche indiquant son sens ! Voici un exemple d'un vecteur totalement mis au hasard dans un repère orthonormé :

Coordonnées : représentation et calcul des coordonnées d'un vecteur
Ce qui est encore plus magique avec un vecteur, c'est qu'il peut avoir des coordonnées ! On peut donc le représenter facilement dans un repère.
Par exemple, je vais prendre le vecteur suivant :
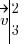
Sans indication complémentaire (on verra plus tard le cas où il y en a, je vous rassure
 ), il vous suffit de prendre un point quelconque de votre repère (pour l'exemple présent je choisis arbitrairement le point de coordonnées
), il vous suffit de prendre un point quelconque de votre repère (pour l'exemple présent je choisis arbitrairement le point de coordonnées 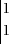 , mais libre à vous d'en choisir un autre à votre convenance
, mais libre à vous d'en choisir un autre à votre convenance  ).
).A partir de ce point, j'ajoute mes coordonnées de vecteur : j'avance donc de 2 sur l'axe des abscisses, et de 3 sur l'axe des ordonnées. Et voilà, le résultat est ci-dessous !

Après, il peut vous être imposé de représenter un vecteur à partir d'un point donné, mais le principe reste identique : vous n'avez qu'à ajouter les coordonnées du vecteur à celles du point imposé pour en trouver la deuxième extrémité !
C'est un peu grâce à cela qu'on peut s'apercevoir qu'il existe autant de possibilités de représenter un vecteur dans un repère que de points dans ce repère, donc... un fort joli paquet !
Lorsque vous avez un couple de points avec leurs coordonnées respectives, vous pouvez également parvenir à calculer l'abscisse et l'ordonnée d'un vecteur correspondant. Ce n'est pas sorcier, mais il faut bien être attentif au sens du vecteur pour ne pas se tromper dans le calcul des coordonnées. Rien de tel qu'un petit exemple pour se faire la main :
Prenons les points suivants :
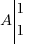 et
et 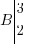
On va immédiatement les positionner dans un repère :

De là, on voit bien que j'ai deux possibilités : soit j'ai le vecteur
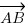 , avec le sens de A vers B, soit le vecteur
, avec le sens de A vers B, soit le vecteur 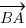 avec le sens de B vers A ! On se décide donc pour s'occuper du vecteur
avec le sens de B vers A ! On se décide donc pour s'occuper du vecteur 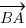 . Alors soyez attentifs : les coordonnées d'un vecteur sont les différences entre les coordonnées de son point d'arrivée et son point de départ.
. Alors soyez attentifs : les coordonnées d'un vecteur sont les différences entre les coordonnées de son point d'arrivée et son point de départ.Pour mon exemple, j'aurai donc l'abscisse de mon vecteur qui sera égale à l'abscisse de B (point d'arrivée) moins l'abscisse de A (point de départ), et pareil pour son ordonnée. En posant le calcul, vous obtenez
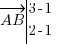 , soit
, soit 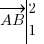
A l'inverse, si j'avais étudié le vecteur
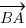 , le calcul des coordonnées aurait été le suivant :
, le calcul des coordonnées aurait été le suivant :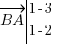 , soit
, soit 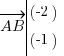 .
.Tiens c'est amusant, vous avez remarqué ? Les coordonnées de ce vecteur sont les opposées de celle du vecteur précédent ! Eh bien oui, lorsqu'on a un vecteur de même direction et de même norme, si son sens change, alors on prend les coordonnées opposées !
Calculs sur les vecteurs
Nous allons aborder ici pas mal de règles différentes à propos du calcul sur les vecteurs, vous verrez là que c'est un outil réellement puissant (niveau mathématique, évidemment
 ).
).Somme de vecteurs
Les vecteurs étant des outils géométriques assez particuliers, il est possible de les ajouter. Prenons un petit exemple, avec sa représentation sur un repère. Ici nous aurons 3 points :
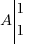 ,
, 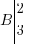 B et
B et 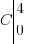 . Mon but est d'ajouter
. Mon but est d'ajouter 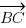 à
à 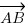 .
.
On va essayer d'imaginer un point qui se déplace. Il part du point A vers le point B (il suit
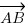 ), puis du point B vers le point C (il suit
), puis du point B vers le point C (il suit 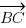 ). J'aurai donc effectué au final le trajet de A vers C. Ajouter deux vecteurs, c'est en fait ajouter leurs coordonnés respectives ! Je vais calculer les coordonnées de mes 2 vecteurs :
). J'aurai donc effectué au final le trajet de A vers C. Ajouter deux vecteurs, c'est en fait ajouter leurs coordonnés respectives ! Je vais calculer les coordonnées de mes 2 vecteurs :D'abord
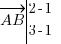 soit
soit 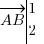 .
.Ensuite,
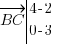 soit
soit 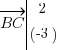 .
.J'ajoute maitenant les coordonnées ainsi trouvées : j'ai 1+2=3 en abscisse, et 2-3=-1 en ordonnée. Calculons à présent les coordonnées du vecteur
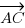 . On a :
. On a :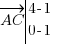 soit
soit 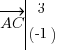 .
.Ca alors, c'est les coordonnées qu'on a trouvé en additionnant les deux vecteurs ! N'est-ce pas magique ? Grâce à cet exemple, non seulement vous savez ajouter deux vecteurs mais vous avez la définition de ce qu'on appelle la relation de Chasles.
C'est une égalité qui vous permet de décomposer un vecteur en une somme de vecteurs. En fait pour tout vecteur
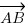 et pour tout point M quelconque du plan, on a l'égalité suivante qui est TOUJOURS vérifiée :
et pour tout point M quelconque du plan, on a l'égalité suivante qui est TOUJOURS vérifiée :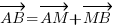 .
.Sinon en passant, comme vous savez maintenant additionner deux vecteurs, vous savez aussi en pratique les soustraire. Ben oui ! Soustraire (souvenez-vous) c'est ajouter l'opposé ! Et les coordonnées de l'opposé d'un vecteur comme on l'a vu pus haut sont les opposées des coordonnées de ce vecteur !
Pour tout vecteur
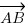 , on peut noter
, on peut noter 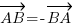
Le vecteur nul
Le vecteur nul est un vecteur qui a 0 en abscisse comme en ordonnée. Reprenons rapidement la dernière ligne précédente :
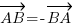 . Si je fais donc
. Si je fais donc 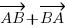 , j'obtiens des coordonnées nulles (ou le vecteur
, j'obtiens des coordonnées nulles (ou le vecteur 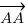 si j'utilise la relation de Chasles, celui-ci aura aussi des coordonnées nulles, voir plus haut). Il est représenté par un 0 surmonté de la flèche typique des vecteurs :
si j'utilise la relation de Chasles, celui-ci aura aussi des coordonnées nulles, voir plus haut). Il est représenté par un 0 surmonté de la flèche typique des vecteurs : 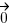 .
.Multiplication d'un nombre par un vecteur
Forcément, si vous pouvez additionner des vecteurs, vous comprendrez bien qu'on peut aussi les multiplier, mais ATTENTION, pas entre eux, uniquement par un nombre !
Si je fais
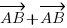 , j'ai bien
, j'ai bien 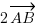 . Pour avoir les coordonnées, il suffit alors de multiplier celles du vecteur d'origine par le nombre en question. Si j'avais ici par exemple
. Pour avoir les coordonnées, il suffit alors de multiplier celles du vecteur d'origine par le nombre en question. Si j'avais ici par exemple 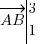 , j'aurai
, j'aurai 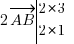 soit
soit 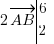 .
.Vecteurs colinéaires
Euh... Si
 J'avoue qu'il y a pas mal de vocabulaire à assimiler, mais là, le principe est assez aisé à comprendre. On dit de deux vecteurs qu'ils sont colinéaires s'ils ont la même direction, tout simplement.
J'avoue qu'il y a pas mal de vocabulaire à assimiler, mais là, le principe est assez aisé à comprendre. On dit de deux vecteurs qu'ils sont colinéaires s'ils ont la même direction, tout simplement.Par exemple, si je prends les points suivants :
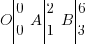 . Les plus fûtés d'entre vous remarqueront qu'on a
. Les plus fûtés d'entre vous remarqueront qu'on a 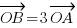 . Eh bien ceux-là ont tout compris (et les autres l'apprennent maintenant
. Eh bien ceux-là ont tout compris (et les autres l'apprennent maintenant  ) : pour que deux vecteurs soient colinéaires, il suffit qu'il existe un coéfficient quelconque qui fait qu'on puisse retrouver les coordonnées de l'un par rapport à l'autre. En formule "mathématique", on dira que deux vecteurs
) : pour que deux vecteurs soient colinéaires, il suffit qu'il existe un coéfficient quelconque qui fait qu'on puisse retrouver les coordonnées de l'un par rapport à l'autre. En formule "mathématique", on dira que deux vecteurs 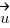 et
et 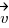 sont colinéaires si et seulement si il existe un nombre k (oui on l'appelle k comme on aurait pu l'appeler Robert ou T, mais bon... je m'égare) tel que
sont colinéaires si et seulement si il existe un nombre k (oui on l'appelle k comme on aurait pu l'appeler Robert ou T, mais bon... je m'égare) tel que 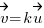 .
.Je vous mets quand même les points de mon exemple, pour que vous voyez que ces points sont bien sur la même direction (ici c'est un cas simple vu que les points sont effectivement alignés, mais vous pourriez très bien avoir des vecteurs de directions parallèles). Voilà le dessin :

Après, quand vous avez les coordonnées de deux vecteurs, il y a une méthode infaillible pour déterminer si ceux-ci sont colinéaires ou pas. On va reprendre nos vecteurs
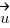 et
et 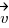 . Ecrivons leurs coordonnées :
. Ecrivons leurs coordonnées : 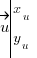 et
et 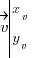 .
.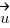 et
et 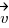 sont colinéaires si et seulement si
sont colinéaires si et seulement si 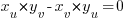 . La preuve avec notre exemple (je vous épargne les calculs des coordonnées, normalement vous savez faire maintenant :
. La preuve avec notre exemple (je vous épargne les calculs des coordonnées, normalement vous savez faire maintenant : ) : j'ai
) : j'ai 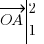 et
et 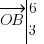 . J'applique ma nouvelle formule : je dois donc calculer 2*3 - 1*6, donc 6-6, donc 0. Mes vecteurs sont bien colinéaires !!
. J'applique ma nouvelle formule : je dois donc calculer 2*3 - 1*6, donc 6-6, donc 0. Mes vecteurs sont bien colinéaires !!Cette partie est importante pour ce qui suivra prochainement, n'hésitez donc pas à faire et refaire des essais pour bien acquérir la technique de vérification de colinéarité.
Vecteurs orthogonaux
La dernière chose à savoir, c'est que grâce aux coordonnées, vous pouvez savoir si deux vecteurs ont leurs directions qui sont orthogonales (pour rappel, qui forment un angle droit). Cette fois, il faut appliquer la formule suivante (je garde les vecteurs et coordonnées du paragraphe précédent) :
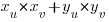 . Si le résultat est nul, vos vecteurs ont leurs directions orthogonales. Un exemple concret ? On prend les points suivants :
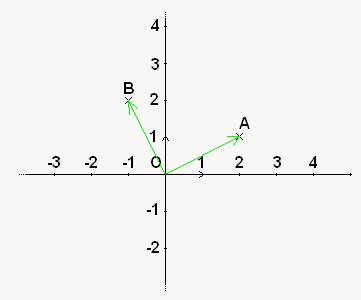
. Si le résultat est nul, vos vecteurs ont leurs directions orthogonales. Un exemple concret ? On prend les points suivants : 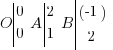
Voici le dessin de tout ça, et même à l'oeil nu vous pouvez voir qu'effectivement, l'angle entre les directions de
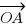 et
et 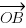 est droit.
est droit.
Je fais à présent le calcul pour confirmer tout ça :
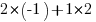 , soit
, soit 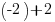 , soit
, soit  .
.Voilà qui démontre que la formule de calcul est bonne !
Equations de droites
Grâce aux vecteurs, nous allons être en mesure de définir une équation (rappelez-vous, une expression contenant un signe "=") pour représenter une droite. Le but est de pouvoir représenter une droite comme un ensemble de points, dont on calcule l'ordonnée en fonction de l'abscisse ! Ce qui est plus qu'utile lorsqu'on souhaite par exemple représenter une trajectoire linéaire.
Le vecteur directeur
Comme son nom l'indique, on peut déterminer un vecteur qui indique la direction d'une droite. Il suffit de prendre deux points (bien placés pour faciliter les calculs) sur la représentation d'une droite, et vous aurez les coordonnées de ce vecteur directeur. Reprenons une représentation de droite déjà vue précédemment :

Cette droite passe par les points A et B, on peut donc dire que
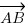 est un vecteur directeur de cette droite. Ses coordonnées sont les suivantes :
est un vecteur directeur de cette droite. Ses coordonnées sont les suivantes :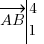
Détermination de l'équation de droite
Méthode des vecteurs colinéaires
Pour déterminer l'équation d'une droite, vous n'avez besoin que des coordonnées de deux points de celle-ci. On va reprendre l'exemple du dessus avec les points
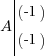 et
et 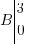
On va partir du principe qu'il y a sur la droite un point
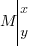 .
.Comme on l'a dit plus haut, le fait que M soit sur la droite implique que les différents vecteurs qu'on peut former avec ces 3 points soient colinéaires. On va donc prendre un vecteur dont on peut déterminer les coordonnées (au hasard le vecteur
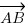 qui est le vecteur directeur), puis un vecteur quelconque, soit
qui est le vecteur directeur), puis un vecteur quelconque, soit 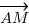 , soit
, soit 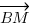 . Par commodité pour les calculs qui vont suivre, je choisis
. Par commodité pour les calculs qui vont suivre, je choisis 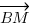 .
.J'ai donc
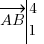 et
et 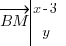 .
.Ces 2 vecteurs étant par définition colinéaires, je peux appliquer ma formule qui permet de vérifier la colinéarité, et ainsi trouver l'égalité suivante, qui est vérifiée !
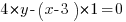 , ce qui équivaut à
, ce qui équivaut à 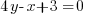 , ou encore, après avoir tout rangé comme il faut :
, ou encore, après avoir tout rangé comme il faut : 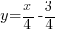
Et voilà, j'ai mon équation de droite ! Les coordonnées de tous les points de la droite vérifieront cette équation. Si vous remplacez les x et y de l'équation respectivement par l'abscisse et l'ordonnée d'un point de la droite, vous aurez toujours une égalité vérifiée. Vous ne me croyez pas ? Eh bien testons avec les deux points connus A et B !
Pour A, je remplace les x et y de l'équation par les "bonnes" coordonnées :
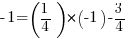 , ce qui me donne
, ce qui me donne 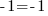 : c'est vérifié !
: c'est vérifié !Idem pour B :
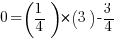 ce qui me donne
ce qui me donne 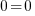 , c'est vérifié aussi !
, c'est vérifié aussi !L'équation de droite peut ainsi vous servir à trouver un point sur la droite si vous ne connaissez que son abscisse ou son ordonnée. Si je cherche par exemple le point de la droite qui a une abscisse nulle, il me suffit de remplacer x par 0 dans l'équation, et je trouve directement l'ordonnée (je vous dispense des calculs, mais si vous les faites, vous trouverez
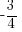 .
.D'ailleurs, l'ordonnée de ce point particulier d'abscisse 0 sur une droite est appelé l'ordonnée à l'origine !
Méthode du coefficient directeur
La majorité des équations de droites (les cas particuliers seront abordés plus bas, ne vous inquiétez pas
 ) sera de la forme
) sera de la forme 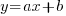 avec a et b, deux nombres quelconques. Le nombre a est appelé coefficient directeur, et b, on l'a déjà vu, c'est l'ordonnée à l'origine. Si vous avez un vecteur directeur d'une droite, et les coordonnées d'un point de cette droite, il est assez facile de déterminer l'équation de celle-ci. Le calcul du coefficient directeur se fait en faisant la division de l'ordonnée du vecteur directeur par son abscisse. Si j'applique ce calcul avec mon exemple précédent, j'avais le vecteur directeur
avec a et b, deux nombres quelconques. Le nombre a est appelé coefficient directeur, et b, on l'a déjà vu, c'est l'ordonnée à l'origine. Si vous avez un vecteur directeur d'une droite, et les coordonnées d'un point de cette droite, il est assez facile de déterminer l'équation de celle-ci. Le calcul du coefficient directeur se fait en faisant la division de l'ordonnée du vecteur directeur par son abscisse. Si j'applique ce calcul avec mon exemple précédent, j'avais le vecteur directeur 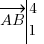 : mon coefficient directeur est donc bien
: mon coefficient directeur est donc bien 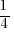 (la preuve, regardez à nouveau l'équation qu'on a trouvé précédemment !).
(la preuve, regardez à nouveau l'équation qu'on a trouvé précédemment !).A partir de là, je sais que mon équation de droite sera de la forme
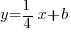 . Après il me reste à prendre les coordonnées d'un point connu de la droite, et de remplacer dans cette dernière équation x et y par les coordonnées du point. Si je prends le point B, je trouve donc :
. Après il me reste à prendre les coordonnées d'un point connu de la droite, et de remplacer dans cette dernière équation x et y par les coordonnées du point. Si je prends le point B, je trouve donc :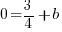 . Je résous l'équation, je trouve
. Je résous l'équation, je trouve 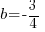 . J'ai donc mon coefficient directeur et mon ordonnée à l'origine : je peux donc écrire mon équation de droite qui est bien
. J'ai donc mon coefficient directeur et mon ordonnée à l'origine : je peux donc écrire mon équation de droite qui est bien 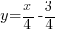
Droites particulières
Comme dit au paragraphe du dessus, il y a certaines droites qui ont des équations pour le moins particulières. Ces droites sont les parallèles aux axes de mon repère ! Eh oui, regardez un peu le dessin suivant, ou je fais passer des droites respectivement parallèle à l'axe des abscisses par le point
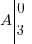 , et à l'axe des ordonnées par le point
, et à l'axe des ordonnées par le point 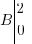 :
:
Pour la droite qui passe par le point A, on remarque que quelle que soit l'abscisse du point de la droite, l'ordonnée sera toujours de 3. L'équation est ici on ne peut plus simple :
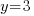 . Eh oui, l'ordonnée ne se calcule pas ici en fonction de l'abscisse, vu qu'elle est constante ! En conclusion, toute droite parallèle à l'axe des abscisses sera de la forme
. Eh oui, l'ordonnée ne se calcule pas ici en fonction de l'abscisse, vu qu'elle est constante ! En conclusion, toute droite parallèle à l'axe des abscisses sera de la forme 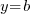 , avec b un nombre quelconque.
, avec b un nombre quelconque.Pour celle qui passe par le point B, c'est pareil, à ceci près que c'est cette fois l'abscisse qui reste constante. Pour mon exemple, l'équation est donc
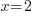 . Donc au final toute droite parallèle à l'axe des ordonnées sera de la forme
. Donc au final toute droite parallèle à l'axe des ordonnées sera de la forme 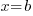 , avec b un nombre quelconque.
, avec b un nombre quelconque.Enfin, il y a une droite à l'équation un peu particulière :
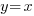 . Sur cette droite (qui passe par l'origine), tous les points ont leurs abscisses et ordonnées égales. En voici la représentation :
. Sur cette droite (qui passe par l'origine), tous les points ont leurs abscisses et ordonnées égales. En voici la représentation :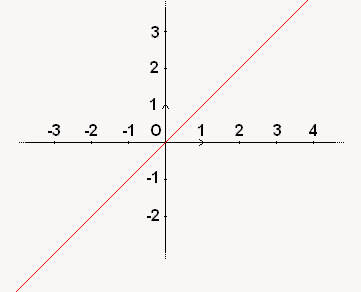
Voilà qui conclut ce chapitre sur les équations de droites !
Pour aller plus loin...
Il aurait été possible d'aller encore plus loin, mais je vais arrêter là ce tutoriel sur les repères. Il est cependant fort probable que vous les retrouviez dans un prochain tuto mathématique, donc ne vous endormez pas sur les acquis.
En fait, pour ceux qui veulent aller plus loin, sachez qu'on peut aussi trouver des équations pour toute une floppée de courbes et formes diverses, mais là on entre dans une méthode un peu plus pointue, qui s'appelle l'étude de fonctions (qui se voit lors des années de première et terminale scientifique), et qui couvre vraiment un champ de possibilités très large. Vous en savez a priori pour le moment assez, vous savez placer des points dans un repère et déterminer des équations de droites, vous avez ainsi un petit bagage intéressant pour aborder sereinement la programmation côté graphique de vos MSX chéris !


