Les équations
Définition d'une équation
Pour définir une équation, on peut dire qu'il s'agit d'une relation d'égalité entre deux choses, qui est vraie, ou vérifiée si vous préférez.
Si je prends l'égalité suivante :
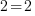 , nous sommes d'accord qu'il s'agit d'une égalité vraie. Si je marque à présent
, nous sommes d'accord qu'il s'agit d'une égalité vraie. Si je marque à présent 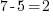 , c'est vrai aussi. De même pour
, c'est vrai aussi. De même pour 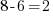 , ou
, ou 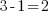 . Vous remarquerez à raison que j'ai choisi des opérations donnant toutes comme résultat 2. En effet, c'est pour vous présenter la notion d'équivalence entre deux équations.
. Vous remarquerez à raison que j'ai choisi des opérations donnant toutes comme résultat 2. En effet, c'est pour vous présenter la notion d'équivalence entre deux équations. 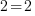 est équivalente à
est équivalente à 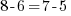 , parce que les deux équations sont deux interprétations de la même égalité vraie.
, parce que les deux équations sont deux interprétations de la même égalité vraie.J'avoue que le vocabulaire est un poil complexe
 , mais je vais essayer de vous aider à assimiler le truc : en fait c'est comme lorsque l'on parle ou écrit : on a parfois plusieurs mots pour décrire la même chose, les synonymes. Après vous pouvez aussi vous représenter ça comme un dictionnaire, où vous avez une explication détaillée pour décrire un seul mot.
, mais je vais essayer de vous aider à assimiler le truc : en fait c'est comme lorsque l'on parle ou écrit : on a parfois plusieurs mots pour décrire la même chose, les synonymes. Après vous pouvez aussi vous représenter ça comme un dictionnaire, où vous avez une explication détaillée pour décrire un seul mot.Par exemple, je prends un exemple culinaire (oui je viens de passer à table
 ). Si je vous dit "pomme de terre coupée en bâtons cuits dans l'huile", vous aurez directement compris de quoi je parle ! Si je pose une équation, j'ai bien :
). Si je vous dit "pomme de terre coupée en bâtons cuits dans l'huile", vous aurez directement compris de quoi je parle ! Si je pose une équation, j'ai bien :frite = pomme de terre coupée en bâtons cuits dans l'huile
Si je vous parle également de "spécialité à base de pomme de terre généralement liée à la Belgique", vous pensez à quoi ?
Je peux donc aussi écrire :
frite = spécialité à base de pomme de terre généralement liée à la Belgique
J'ai donc bien deux égalités qui sont équivalentes : frite = pomme de terre coupée en bâtons cuits dans l'huile équivaut à frite = spécialité à base de pomme de terre généralement liée à la Belgique.
Ce sont bien deux manières différentes d'énoncer la même chose !

Maintenant, les équations en mathématiques, ce n'est pas si simple, et elles ont un but précis, c'est ce que nous allons voir à présent.
La recherche de l'inconnue
Ne rêvez pas, les équations qu'on va aborder ne seront pas du type
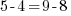 , ce serait bien trop facile ! En fait, les équations mathématiques sont toujours posées avec une ou plusieurs lettres. Un exemple ?
, ce serait bien trop facile ! En fait, les équations mathématiques sont toujours posées avec une ou plusieurs lettres. Un exemple ?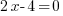
Le but de la résolution d'équation est là : chercher la (ou les) valeurs de x pour que l'équation soit vraie !
Surtout pas malheureux !!
 Ce serait un travail bien trop lourd et fastidieux ! La méthode pour résoudre une équation, c'est de trouver des équations équivalentes, jusqu'à ce qu'on puisse trouver directement la valeur de x. Mais tout ceci va être expliqué au paragraphe suivant !
Ce serait un travail bien trop lourd et fastidieux ! La méthode pour résoudre une équation, c'est de trouver des équations équivalentes, jusqu'à ce qu'on puisse trouver directement la valeur de x. Mais tout ceci va être expliqué au paragraphe suivant ! 
Résoudre une équation c'est respecter la vérité !
Eh oui, comme le titre l'indique, résoudre une équation, c'est aussi simple que ça ! Je vais reprendre mon exemple hyper simple du début :
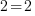 .
.Si vous appliquez la même opération de chaque côté du terme "=", vous vous rendrez compte qu'on garde une équation vraie ! Je vous illustre ça tout de suite, en appliquant une première opération arithmétique classique : l'addition d'un nombre. Quel nombre prend-on ? 5 ça vous va ? OK alors vérifions :
Est-ce que j'ai bien
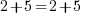 ? Soit
? Soit 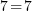 ? Oui, donc je peux ajouter 5 de chaque côté de mon égalité, la vérité est respectée.
? Oui, donc je peux ajouter 5 de chaque côté de mon égalité, la vérité est respectée.Avec la soustraction ? Même principe : je retire 1 de chaque côté :
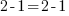 ?
? 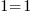 ? Bien sûr ! La vérité est respectée aussi !
? Bien sûr ! La vérité est respectée aussi !Et si on multipliait à présent ? Par 7 par exemple ?
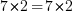 ? Je ne prends même plus la peine de vous donner le résultat
? Je ne prends même plus la peine de vous donner le résultat 
Et il en va de même pour la division : en divisant les deux termes par 2, j'aurai
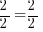 , donc
, donc 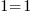 , toujours la vérité !
, toujours la vérité !Pour toute équation vous aurez donc la possibilité d'effectuer les mêmes opérations arithmétiques de chaque côté du signe "=", vous obtiendrez une équation équivalente ! Avec une équation à une inconnue, notre but sera donc ce qu'on appelle isoler l'inconnue, soit la mettre toute seule d'un côté du signe "=". Pour réaliser ça, je vais devoir faire en sorte d'appliquer aux termes de l'égalité des opérations "opposées" à celles présentes dans l'équation. Si j'ai une addition, j'applique une soustraction et inversement. Si c'est une division, je fais une multiplication, et inversement.
On se résout l'équation du paragraphe précédent pour avoir un exemple concret ?
J'ai
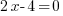 . Ici, J'ai d'abord l'inconnue qui est multipliée par 2. On lui retranche ensuite 4. J'ai donc une multiplication et une soustraction. Je vais commencer par "éliminer" la soustraction : je vais donc additionner 4 de chaque côté de l'égalité. J'obtiens donc :
. Ici, J'ai d'abord l'inconnue qui est multipliée par 2. On lui retranche ensuite 4. J'ai donc une multiplication et une soustraction. Je vais commencer par "éliminer" la soustraction : je vais donc additionner 4 de chaque côté de l'égalité. J'obtiens donc :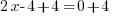 , soit
, soit 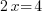 . A présent, je vais "éliminer" la multiplication par 2 en divisant par 2 les deux côtés :
. A présent, je vais "éliminer" la multiplication par 2 en divisant par 2 les deux côtés :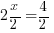 , soit
, soit 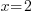 . Mais ? Mais ?!? Mais j'ai la valeur de mon inconnue !! Certes, on est arrivé à isoler correctement l'inconnue, mais avant d'aller crier partout sur les toits sa valeur, il faut vérifier dans l'équation de départ, pour être bien sûr de ne pas avoir raté quelque chose :
. Mais ? Mais ?!? Mais j'ai la valeur de mon inconnue !! Certes, on est arrivé à isoler correctement l'inconnue, mais avant d'aller crier partout sur les toits sa valeur, il faut vérifier dans l'équation de départ, pour être bien sûr de ne pas avoir raté quelque chose :Si je prends comme valeur 2 pour x, j'ai dans mon équation de départ :
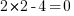 , soit
, soit 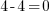 , soit
, soit 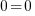 : j'obtiens bien une équation vraie, je peux donc clamer haut et fort que ma solution est 2 !
: j'obtiens bien une équation vraie, je peux donc clamer haut et fort que ma solution est 2 ! 
Ici l'exemple était simple, forcément c'est pour l'exemple. Et si vous tentiez le coup tout seul pour voir, sur une équation un peu plus dure ?
Allez tiens, résolvez-moi celle-ci :
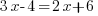 .
.Aha ! On fait moins le malin ?
 Blague à part, essayez de résoudre celle-ci par vous-même, sachant que vous pouvez additionner et soustraire ce que vous voulez des deux côtés de l'égalité, même l'inconnue et des multiples de celle-ci...
Blague à part, essayez de résoudre celle-ci par vous-même, sachant que vous pouvez additionner et soustraire ce que vous voulez des deux côtés de l'égalité, même l'inconnue et des multiples de celle-ci...La solution est cachée, si vous voulez voir le détail, il n'y a qu'à cliquer !
Caché :
Première étape : je me débarrasse de la soustraction du terme de gauche : j'ajoute donc 4 de chaque côté, j'obtiens :
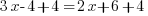 , soit
, soit 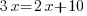 .
.
Deuxième étape : je regroupe tout ce qui concerne l'inconnue du même côté. Je vais donc retirer de chaque côté 2x. Eh oui ! On a donc :
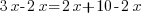 , soit
, soit 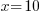 .
.
Troisième étape : vérification de ma solution : je vérifie si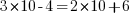 .
.
J'ai donc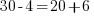 soit
soit 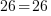 , tout est OK, la solution de l'équation est bien 10 !
, tout est OK, la solution de l'équation est bien 10 !
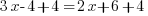 , soit
, soit 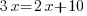 .
.Deuxième étape : je regroupe tout ce qui concerne l'inconnue du même côté. Je vais donc retirer de chaque côté 2x. Eh oui ! On a donc :
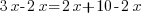 , soit
, soit 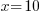 .
.Troisième étape : vérification de ma solution : je vérifie si
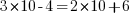 .
.J'ai donc
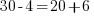 soit
soit 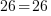 , tout est OK, la solution de l'équation est bien 10 !
, tout est OK, la solution de l'équation est bien 10 !Habituellement, en mathématiques, on a coutume de donner la solution sous forme d'un ensemble. Dans le cadre des mathématiques pour la programmation, il n'est pas essentiel que vous le sachiez mais pour information c'est toujours intéressant de le savoir. On appelle donc S l'ensemble des solutions, et la réponse est placée entre accolades. La notation est la suivante :
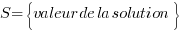
Une solution seule, comme c'est souvent le cas ici est appelée un singleton
Cas particuliers
Bien sûr, il existe des cas particuliers pour certaines équations, sinon ce serait trop facile.
 Heureusement, il n'y a que deux cas qui peuvent se présenter :
Heureusement, il n'y a que deux cas qui peuvent se présenter :1er cas : pas de solution
Vous n'aurez pas de solution lorsque, quelle que soit la valeur de l'inconnue, l'équation est fausse. Je vous donne immédiatement un exemple de ce cas très particulier. Si je vous pose l'équation suivante :
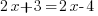 .
.Tentons alors de la résoudre :
Je regroupe d'abord les nombres du côté droit de l'égalité, j'ajoute donc 4 de chaque côté, j'obtiens :
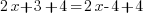 soit
soit 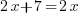
A présent je regroupe tout ce qui concerne l'inconnue du même côté, je dois donc retirer 2x de chaque côté. J'obtiens :
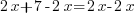 soit
soit 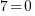
Il n'y a pas quelque chose qui vous perturbe là ?
 En effet, on obtient quoi qu'il arrive une égalité fausse : cette équation n'a donc aucune solution possible !
En effet, on obtient quoi qu'il arrive une égalité fausse : cette équation n'a donc aucune solution possible !2ème cas : une infinité de solutions
Les équations qui ont une infinité de solutions sont facilement reconnaissables, en effet, les deux côtés de l'égalité sont identiques en valeur numérique ! Par exemple, l'équation suivante,
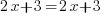 comporte une infinité de solutions ! Tentez de remplacer x par n'importe quelle valeur et vérifiez l'égalité, vous verrez par vous-même le résultat !
comporte une infinité de solutions ! Tentez de remplacer x par n'importe quelle valeur et vérifiez l'égalité, vous verrez par vous-même le résultat !Voilà qui conclut ce qui concerne les équations à une inconnue ! Forts de cette nouvelle connaissance, on va pouvoir attaquer la deuxième partie : les inéquations !
Les inéquations
Définition d'une inéquation
A l'instar des équations, une inéquation représente un énoncé vrai. La seule chose qui change, c'est qu'on n'a plus cette fois d'égalité, mais une inégalité ! Les signes qui seront utilisés ici sont donc les suivants :
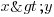 : soit "x est supérieur à y"
: soit "x est supérieur à y"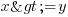 : soit "x est supérieur ou égal à y"
: soit "x est supérieur ou égal à y"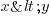 : soit "x est inférieur à y"
: soit "x est inférieur à y"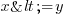 : soit "x est inférieur ou égal à y"
: soit "x est inférieur ou égal à y"La notion d'infériorité ou supériorité avec égalité signifiant bien sûr que l'égalité est tolérée (par exemple
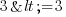 est considérée comme vraie, contrairement à
est considérée comme vraie, contrairement à 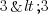 qui n'est pas vraie).
qui n'est pas vraie).La recherche des inconnues
Là est toute la différence avec une équation : ici pour les inéquations on ne cherche pas la valeur d'une inconnue, mais une plage de valeurs qui permette de conserver la vérité de l'expression. Pour une inéquation simple, comme
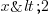 , x peut avoir la valeur 1, l'expression est vraie. Mais si x prend la valeur 0, celle-ci est également vraie. Je pourrais vous donner encore plein de solutions possibles, mais bon on a pas la vie devant nous !
, x peut avoir la valeur 1, l'expression est vraie. Mais si x prend la valeur 0, celle-ci est également vraie. Je pourrais vous donner encore plein de solutions possibles, mais bon on a pas la vie devant nous !  En effet, pour cette équation si basique, le nombre de solutions est infini ! Eh oui, absolument TOUS les nombres plus petits que 2 sont solution ! De 0,5 à -10253 en passant par 1,75 ou -8944544586, ces nombres sont solutions de l'inéquation !
En effet, pour cette équation si basique, le nombre de solutions est infini ! Eh oui, absolument TOUS les nombres plus petits que 2 sont solution ! De 0,5 à -10253 en passant par 1,75 ou -8944544586, ces nombres sont solutions de l'inéquation !Au final, on peut dire que pour une inéquation, on aura bien un ensemble de solutions !
Résolution d'une inéquation : attention au signe !
La méthode de résolution d'une inéquation est exactement la même que pour une équation : le but de la manoeuvre sera toujours de parvenir à isoler l'inconnue d'un côté de l'inégalité, en appliquant des opérations arithmétiques sur l'inégalité. Tout se passe bien pour l'addition et la soustraction, mais il y a une précaution à prendre pour ce qui est multiplication et division ! Avec les exemples suivants, vous allez comprendre :
Prenons deux nombres positifs quelconques : on va faire simple, avec 2 et 1.
Je peux écrire
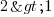 , car c'est une expression vérifiée. Que se passe-t-'il lorsque je prends leurs opposés ? Eh bien cette fois j'ai
, car c'est une expression vérifiée. Que se passe-t-'il lorsque je prends leurs opposés ? Eh bien cette fois j'ai 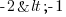 ... Eh oui, quand il fait -10°C dehors, la température est bien moins élevée que lorsqu'il fait -1°C ! Avec les nombres négatifs, plus la valeur du nombre après le signe - est élevée, plus le nombre est petit ! Cela impacte directement le signe de notre inéquation lorsqu'on multiplie ou divise par un nombre négatif. Pour notre exemple, en prenant les opposés, on peut dire que j'ai effectué une multiplication des deux termes par -1. Avec une multiplication par -1 je passe de
... Eh oui, quand il fait -10°C dehors, la température est bien moins élevée que lorsqu'il fait -1°C ! Avec les nombres négatifs, plus la valeur du nombre après le signe - est élevée, plus le nombre est petit ! Cela impacte directement le signe de notre inéquation lorsqu'on multiplie ou divise par un nombre négatif. Pour notre exemple, en prenant les opposés, on peut dire que j'ai effectué une multiplication des deux termes par -1. Avec une multiplication par -1 je passe de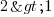
à
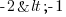
ou, si vous préférez garder le même signe d'inégalité :
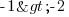
En résumé : dans une inéquation, lorsqu'on multiplie ou divise par un nombre négatif, soit on change le signe d'inégalité, soit on inverse les deux termes de l'inégalité.
Retenez bien ceci car c'est capital pour ne pas faire d'erreur !!

On va passer à quelques exemples de résolution d'inéquations, ensemble d'abord, puis vous essaierez seuls ensuite.
Exercice 1 : Résoudre l'inéquation
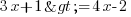
1ère étape : on se débarrasse du nombre dans la partie de gauche de l'inégalité. Je retranche donc 1 de chaque côté. J'ai donc
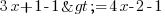 soit
soit 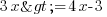
2ème étape : on regroupe ce qui concerne l'inconnue dans la partie de gauche de l'inégalité. Je retranche donc 4x de chaque côté. J'ai donc
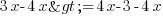 soit
soit 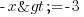
3ème étape : je termine en multipliant par -1 de chaque côté pour obtenir x et non plus -x. J'ai donc
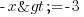 qui devient
qui devient 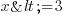
J'ai donc a priori tous les nombres inférieurs ou égaux à 3 qui satisfont l'inégalité. On peut donc vérifier à présent, en prenant x=0 par exemple. Ai-je bien
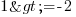 ? Oui, donc ma solution est bonne !
? Oui, donc ma solution est bonne !On présente la solution sous forme d'un ensemble, avec des crochets, sous la forme [borne inférieure de l'ensemble; borne supérieure de l'ensemble]. Comme il y a une infinité de solutions, on utilise un symbole pour décrire l'infini. Celui-ci se présente sous la forme d'un 8 couché :
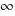 . Et en mathématiques, il y a deux infinis : l'infini positif noté
. Et en mathématiques, il y a deux infinis : l'infini positif noté 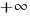 , et l'infini négatif noté
, et l'infini négatif noté 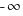 .
.Le sens des crochets dans la représentation de l'ensemble est important également : il indique si on exclut une borne ou pas.
Le crochet de gauche, lorsqu'il est ouvrant (" [ ") indique qu'on inclut la borne inférieure.
Lorsqu'il est fermant (" ] "), il indique qu'on exclut la borne inférieure.
Et inversement, le crochet droit lorsqu'il est ouvrant indique qu'on exclut la borne supérieure, et qu'on l'inclut lorsqu'il est fermant.
Pour info, une borne infinie est [b]toujours[b] exclue.
Pour notre exemple, on note donc S l'ensemble des solutions, on a donc
![S=]-infty;3] S=]-infty;3]](/images/maths/math_982_8dceb91cb7f58a4086b686a6f55410ca.png) .
.Vous remarquez donc que la borne 3 est incluse dans l'ensemble, car la borne 3 satisfait l'inéquation. Si on avait eu l'inéquation
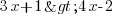 , il aurait fallu exclure la borne 3.
, il aurait fallu exclure la borne 3.Allez, maintenant à vous de travailler, même si je laisse encore une fois la solution à disposition !
Trouvez les solutions de l'inéquation suivante :
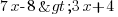
Caché :
1ère étape : on se débarrasse du nombre dans la partie de gauche de l'inégalité. J'ajoute donc 8 de chaque côté. J'ai donc
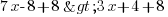 soit
soit 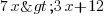
2ème étape : on regroupe ce qui concerne l'inconnue dans la partie de gauche de l'inégalité. Je retranche donc 3x de chaque côté. J'ai donc
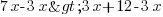 soit
soit 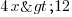
3ème étape : je termine en divisant par 4 de chaque côté. 4 étant positif, pas besoin de changer le signe ! On a donc :
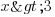
L'ensemble des solutions apparaît être![S=]3; +infty[ S=]3; +infty[](/images/maths/math_982_42e1928e0ec8322288b5e01978c49b63.png) . Je vérifie avec un nombre de cet ensemble (par exemple 5) : ai-je bien
. Je vérifie avec un nombre de cet ensemble (par exemple 5) : ai-je bien 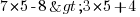 ? Soit
? Soit 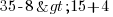 ou encore
ou encore  . La vérité de l'inégalité est bien respectée, mon ensemble de solutions est le bon !
. La vérité de l'inégalité est bien respectée, mon ensemble de solutions est le bon !
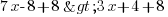 soit
soit 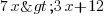
2ème étape : on regroupe ce qui concerne l'inconnue dans la partie de gauche de l'inégalité. Je retranche donc 3x de chaque côté. J'ai donc
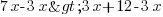 soit
soit 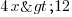
3ème étape : je termine en divisant par 4 de chaque côté. 4 étant positif, pas besoin de changer le signe ! On a donc :
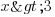
L'ensemble des solutions apparaît être
![S=]3; +infty[ S=]3; +infty[](/images/maths/math_982_42e1928e0ec8322288b5e01978c49b63.png) . Je vérifie avec un nombre de cet ensemble (par exemple 5) : ai-je bien
. Je vérifie avec un nombre de cet ensemble (par exemple 5) : ai-je bien 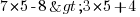 ? Soit
? Soit 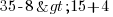 ou encore
ou encore  . La vérité de l'inégalité est bien respectée, mon ensemble de solutions est le bon !
. La vérité de l'inégalité est bien respectée, mon ensemble de solutions est le bon !Vous voilà maintenant expert en équations et inéquations ! Vous me demanderez peut-être à quoi cela va vous servir pour programmer ? Eh bien vous le découvrirez dans d'autres chapitres, notamment celui concernant les repères.
N'hésitez pas à critiquer et à faire des remarques, ce tutoriel n'est pas figé et ne demande qu'à être amélioré !